特征向量和特征值，更深层次的理解镇关西|金绳|执着|名闻|玉锁

文章插图
任何具有特征向量的矩阵，其所有坐标最终都将遵循一个尽可能接近特征向量的关系。为了进一步说明这一点，我将使用一些例子。
斐波那契数列斐波那契数列就是前面两项的和作为第三项。如果我们从0和1开始这个数列：

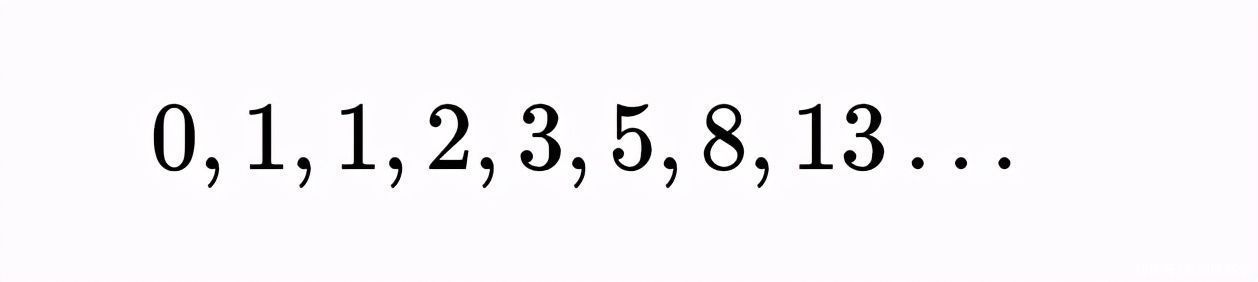
文章插图
直到无穷大。如果我们在笛卡尔坐标系中绘制它，我们可以用一个向量和一个方阵来给出斐波那契数列的下一个值：

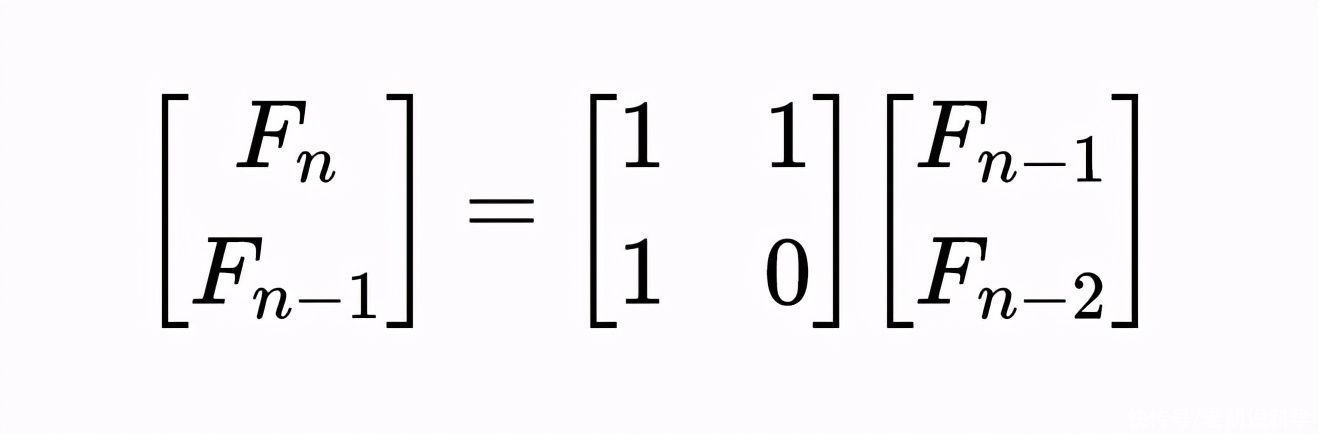
文章插图
第一行表示斐波那契数列中的下一个值，而第二行表示数中的当前值。如果我们画出这个图，我们可以看到每个值大约是之前值的1.618倍。如果我们从0和1开始，第10个值是55，第11个值是89。我们还可以看到55乘以1.618大约等于89。如果我们计算这个向量的特征值，它们是-0.618和1.618。特征值所对应的特征向量分别是：

文章插图

文章插图
这一数列不仅将遵循这一趋势（其中一项是前一项的1.618倍），而且它也会在这样一条直线上，这条直线沿着一个向量，这个向量具有特征值1.618。通过这个，我们可以理解这里的特征的重要性，如果用矩阵的形式写，最终会遵循由其特征值和特征向量定义的特征。根据这一点，我们可以很容易地推导出下一项的值，随着项数的增加，这个值越来越精确。
这不仅可以通过初始值0和1实现，对于任何初始值都可以。我们将看到与下一项增加的因子相同的特征值的数列。当它们增加时，这些值也将接近表示系统中特征向量的直线。
人口增长模型在20世纪40年代，莱斯利找到了一种为人口增长建模的方法，通过这种方法，我们可以相对准确地找到人口增长的情况。莱斯利矩阵是关于特定物种的繁殖率概率和生存机会的函数。莱斯利矩阵是通过将各自的值放入矩阵中形成的：

文章插图
其中，n是总人口的阶段数，F是总体中女性的数量，P是属于第一个阶段的成员进入下一个阶段的概率。我们只选取女性群体，因为她们是特定群体中负责繁殖的群体。我们把这个矩阵代入矩阵方程：

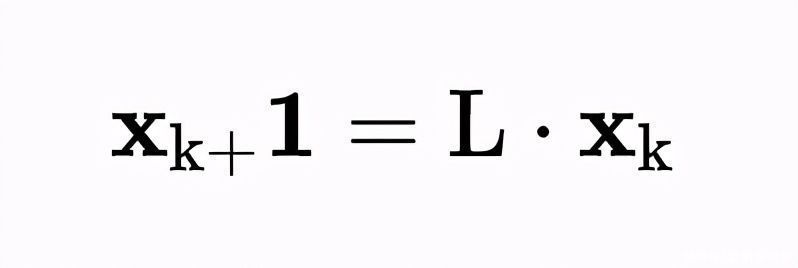
文章插图
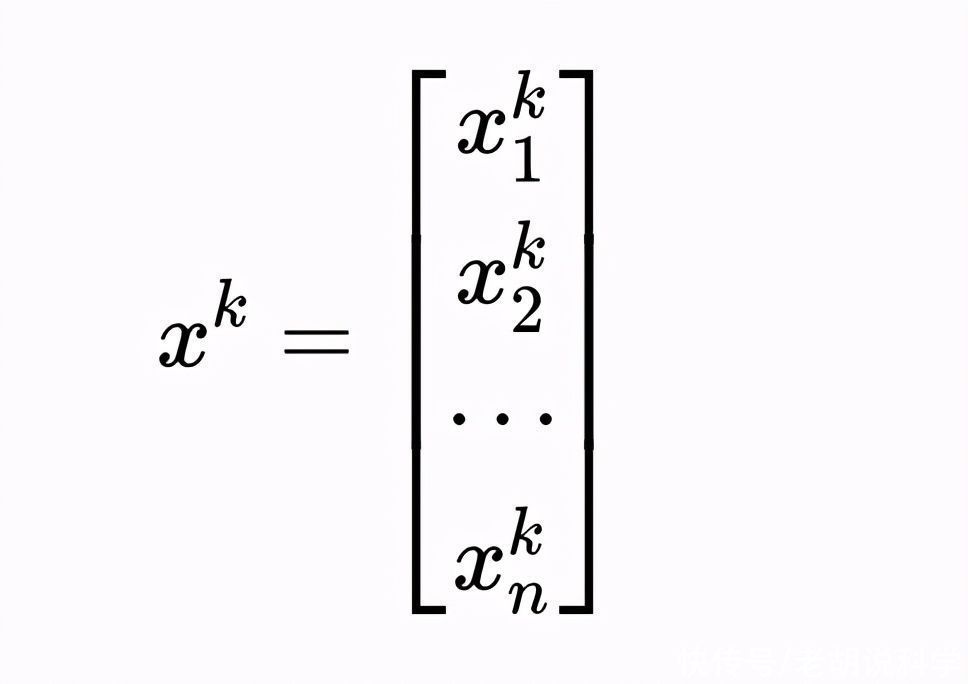
其中x?是矩阵：

文章插图
【特征向量和特征值，更深层次的理解】这个矩阵中的k值表示我们处理初始总体的年份，n是总体被分割的阶段数。这个方程是用以下逻辑推导出来的：

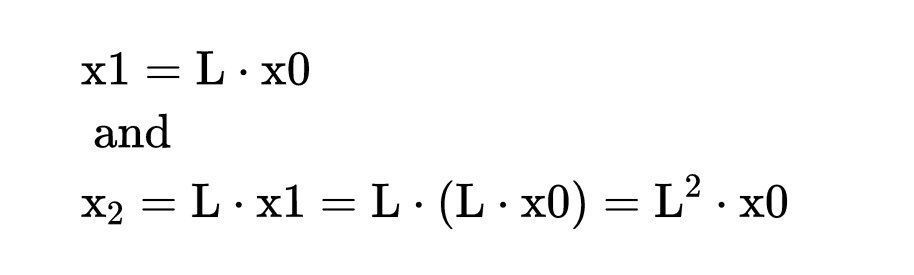
文章插图
虽然用这个矩阵方程我们可以很容易地计算出人口增长，但对于k值较大的情况，需要进行大量的计算，因此我们可以找到系统的特征向量和相应的特征值。通过这样我们得到了系统增长的总体趋势，最终我们可以很容易地计算出k值较大时 x_k的值。
解微分方程组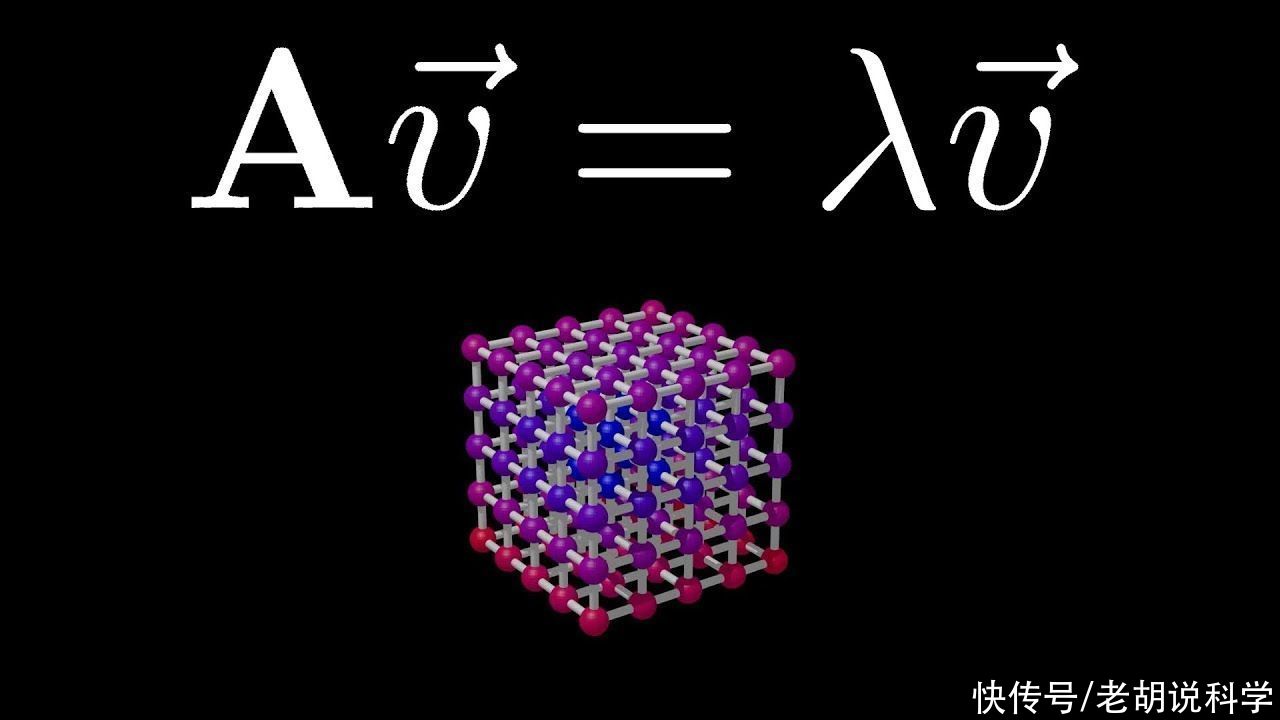

文章插图
通过在增广矩阵中放入适当的值，我们可以利用特征值及其特征向量来求解微分方程组。首先找到增广矩阵的特征值后，我们将它们排列成对角矩阵（D）的形式，其对角项就是特征值。然后我们找到相应的特征向量，并将其排列在一个矩阵（P）中。
我们将对角矩阵代入方程u = Du '中，u是方程组的解。还需要注意的是，D向量是通过系统在每次迭代中发生的变化来表示的，因此它也表示了系统的变化率。一旦我们找到u，我们把它放入方程y = Pu，其中P是包含特征向量的矩阵。矩阵P会告诉我们在每次迭代中值是如何变化的一般方向，当我们将这些值相乘时，我们就能得到方程组（y）的解。