特征工程与模型调优( 五 ) 机器学习特征工程机器学习流程与概念机

文章插图
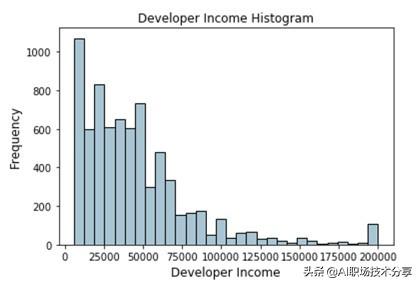
描述开发者收入分布的直方图
上述的分布描述了一个在收入上右歪斜的分布，少数人赚更多的钱，多数人赚更少的钱。让我们基于自适应分箱方式做一个 4-分位数或分位数。我们可以很容易地得到如下的分位数。
quantile_list = [0, .25, .5, .75, 1.]quantiles =fcc_survey_df['Income'].quantile(quantile_list)quantiles**Output****------**0.00 6000.00.25 20000.00.50 37000.00.75 60000.01.00 200000.0Name: Income, dtype: float64现在让我们在原始的分布直方图中可视化下这些分位数。
fig, ax = plt.subplots()fcc_survey_df['Income'].hist(bins=30, color='#A9C5D3',edgecolor='black',grid=False)for quantile in quantiles:qvl = plt.axvline(quantile, color='r')ax.legend([qvl], ['Quantiles'], fontsize=10)ax.set_title('Developer Income Histogram with Quantiles',fontsize=12)ax.set_xlabel('Developer Income', fontsize=12)ax.set_ylabel('Frequency', fontsize=12)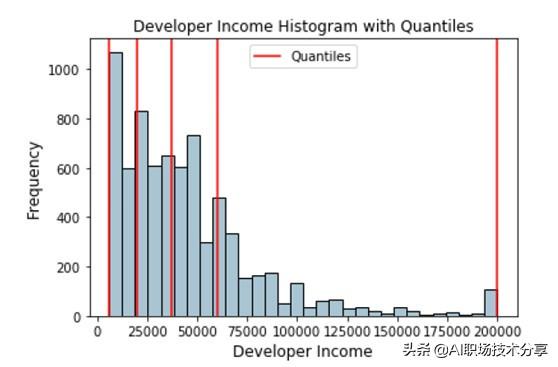
文章插图
带分位数形式描述开发者收入分布的直方图上面描述的分布中红色线代表了分位数值和我们潜在的区间。让我们利用这些知识来构建我们基于分区间策略的分位数。
quantile_labels = ['0-25Q', '25-50Q', '50-75Q', '75-100Q']fcc_survey_df['Income_quantile_range'] = pd.qcut(fcc_survey_df['Income'],q=quantile_list)fcc_survey_df['Income_quantile_label'] = pd.qcut(fcc_survey_df['Income'],q=quantile_list,labels=quantile_labels)fcc_survey_df[['ID.x', 'Age', 'Income','Income_quantile_range','Income_quantile_label']].iloc[4:9]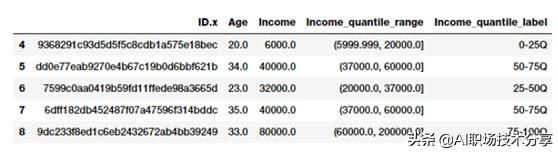
文章插图
基于分位数的开发者收入的区间范围和标签通过这个例子，你应该对如何做基于分位数的自适应分区间法有了一个很好的认识。一个需要重点记住的是，分区间的结果是离散值类型的分类特征，当你在模型中使用分类数据之前，可能需要额外的特征工程相关步骤。我们将在接下来的部分简要地讲述分类数据的特征工程技巧。
统计变换我们讨论下先前简单提到过的数据分布倾斜的负面影响。现在我们可以考虑另一个特征工程技巧，即利用统计或数学变换。我们试试看 Log 变换和 Box-Cox 变换。这两种变换函数都属于幂变换函数簇，通常用来创建单调的数据变换。它们的主要作用在于它能帮助稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。
Log变换log 变换属于幂变换函数簇。该函数用数学表达式表示为
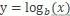文章插图
【特征工程与模型调优】读为以 b 为底 x 的对数等于 y 。这可以变换为
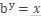文章插图
表示以b为底指数必须达到多少才等于x 。自然对数使用 b=e ， e=2.71828 ，通常叫作欧拉常数。你可以使用通常在十进制系统中使用的 b=10 作为底数。
当应用于倾斜分布时 Log 变换是很有用的，因为他们倾向于拉伸那些落在较低的幅度范围内自变量值的范围，倾向于压缩或减少更高幅度范围内的自变量值的范围。从而使得倾斜分布尽可能的接近正态分布。让我们对先前使用的开发者数据集的 Income 特征上使用log变换。