特征工程与模型调优( 六 ) 机器学习特征工程机器学习流程与概念机

fcc_survey_df['Income_log'] = np.log((1+fcc_survey_df['Income']))fcc_survey_df[['ID.x', 'Age', 'Income','Income_log']].iloc[4:9]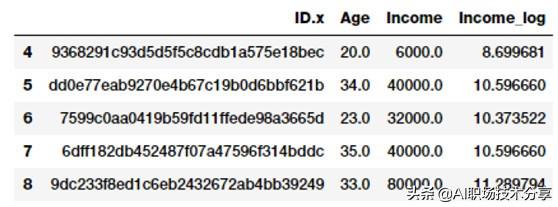
文章插图
开发者收入log变换后结构Income_log 字段描述了经过 log 变换后的特征。现在让我们来看看字段变换后数据的分布。
基于上面的图，我们可以清楚地看到与先前倾斜分布相比，该分布更加像正态分布或高斯分布。
income_log_mean =np.round(np.mean(fcc_survey_df['Income_log']), 2)fig, ax = plt.subplots()fcc_survey_df['Income_log'].hist(bins=30,color='#A9C5D3',edgecolor='black',grid=False)plt.axvline(income_log_mean, color='r')ax.set_title('Developer Income Histogram after Log Transform',fontsize=12)ax.set_xlabel('Developer Income (log scale)',fontsize=12)ax.set_ylabel('Frequency', fontsize=12)ax.text(11.5, 450, r'$\mu$='+str(income_log_mean),fontsize=10)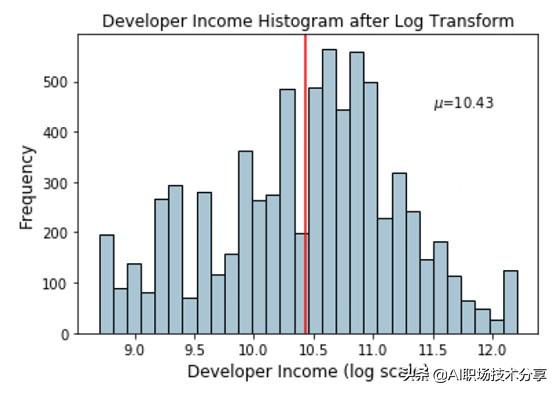
文章插图
经过log变换后描述开发者收入分布的直方图
Box-Cox变换Box-Cox 变换是另一个流行的幂变换函数簇中的一个函数。该函数有一个前提条件，即数值型值必须先变换为正数（与 log 变换所要求的一样）。万一出现数值是负的，使用一个常数对数值进行偏移是有帮助的。数学上， Box-Cox 变换函数可以表示如下。
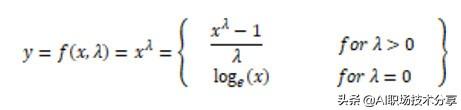文章插图
生成的变换后的输出y是输入 x 和变换参数的函数；当 λ=0 时，该变换就是自然对数 log 变换，前面我们已经提到过了。 λ 的最佳取值通常由最大似然或最大对数似然确定。现在让我们在开发者数据集的收入特征上应用 Box-Cox 变换。首先我们从数据分布中移除非零值得到最佳的值，结果如下。
income = np.array(fcc_survey_df['Income'])income_clean = income[~np.isnan(income)]l, opt_lambda = spstats.boxcox(income_clean)print('Optimal lambda value:', opt_lambda)**Output****------**Optimal lambda value: 0.117991239456现在我们得到了最佳的值，让我们在取值为 0 和 λ（最佳取值 λ ）时使用 Box-Cox 变换对开发者收入特征进行变换。
fcc_survey_df['Income_boxcox_lambda_0'] = spstats.boxcox((1+fcc_survey_df['Income']),lmbda=0)fcc_survey_df['Income_boxcox_lambda_opt'] = spstats.boxcox(fcc_survey_df['Income'],lmbda=opt_lambda)fcc_survey_df[['ID.x', 'Age', 'Income', 'Income_log','Income_boxcox_lambda_0','Income_boxcox_lambda_opt']].iloc[4:9]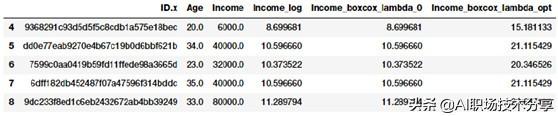
文章插图
经过 Box-Cox 变换后开发者的收入分布变换后的特征在上述数据框中描述了。就像我们期望的那样， Income_log 和 Income_boxcox_lamba_0具有相同的取值。让我们看看经过最佳λ变换后 Income 特征的分布。
123456789101112131415>income_boxcox_mean = np.round(np.mean(fcc_survey_df['Income_boxcox_lambda_opt']),2)> >fig, ax = plt.subplots()> >fcc_survey_df['Income_boxcox_lambda_opt'].hist(bins=30, color='#A9C5D3',edgecolor='black', grid=False)> plt.axvline(income_boxcox_mean, color='r')>> ax.set_title('Developer Income Histogram after Box–Cox Transform',fontsize=12)>> ax.set_xlabel('Developer Income (Box–Cox transform)',fontsize=12)>> ax.set_ylabel('Frequency', fontsize=12)>> ax.text(24, 450, r'$\mu$='+str(income_boxcox_mean),fontsize=10) >