特征工程与模型调优( 三 ) 机器学习特征工程机器学习流程与概念机

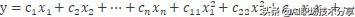文章插图
此处特征可表示为
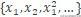文章插图
表示了相关特征。现在让我们试着在 Pokemon 数据集上设计一些相关特征。
atk_def = poke_df[['Attack', 'Defense']]atk_def.head()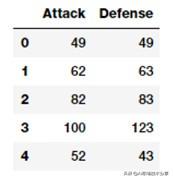
文章插图
从输出数据框中，我们可以看到我们有两个数值型（连续的）特征， Attack 和 Defence 。现在我们可以利用 scikit-learn 建立二度特征。
pf = PolynomialFeatures(degree=2,interaction_only=False,include_bias=False)res = pf.fit_transform(atk_def)res**Output****------**array([[ 49., 49., 2401., 2401., 2401.],[ 62., 63., 3844., 3906., 3969.],[ 82., 83., 6724., 6806., 6889.],...,[ 110., 60., 12100., 6600., 3600.],[ 160., 60., 25600., 9600., 3600.],[ 110., 120., 12100., 13200., 14400.]])上面的特征矩阵一共描述了 5 个特征，其中包括新的相关特征。我们可以看到上述矩阵中每个特征的度，如下所示。
pd.DataFrame(pf.powers_, columns=['Attack_degree','Defense_degree'])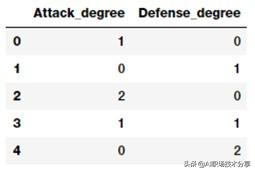
文章插图
基于这个输出，现在我们可以通过每个特征的度知道它实际上代表什么。在此基础上，现在我们可以对每个特征进行命名如下。这仅仅是为了便于理解，你可以给这些特征取更好的、容易使用和简单的名字。
intr_features = pd.DataFrame(res, columns=['Attack','Defense','Attack^2','Attack x Defense','Defense^2'])intr_features.head(5)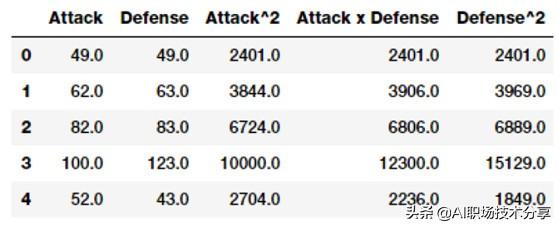
文章插图
数值型特征及其相关特征因此上述数据代表了我们原始的特征以及它们的相关特征。
分区间处理数据处理原始、连续的数值型特征问题通常会导致这些特征值的分布被破坏。这表明有些值经常出现而另一些值出现非常少。除此之外，另一个问题是这些特征的值的变化范围。比如某个音乐视频的观看总数会非常大（Despacito ，说你呢）而一些值会非常小。直接使用这些特征会产生很多问题，反而会影响模型表现。因此出现了处理这些问题的技巧，包括分区间法和变换。
分区间（Bining），也叫做量化，用于将连续型数值特征转换为离散型特征（类别）。可以认为这些离散值或数字是类别或原始的连续型数值被分区间或分组之后的数目。每个不同的区间大小代表某种密度，因此一个特定范围的连续型数值会落在里面。对数据做分区间的具体技巧包括等宽分区间以及自适应分区间。我们使用从 2016 年 FreeCodeCamp 开发者和编码员调查报告中抽取出来的一个子集中的数据，来讨论各种针对编码员和软件开发者的属性。
fcc_survey_df =pd.read_csv('datasets/fcc_2016_coder_survey_subset.csv',encoding='utf-8')fcc_survey_df[['ID.x', 'EmploymentField', 'Age','Income']].head()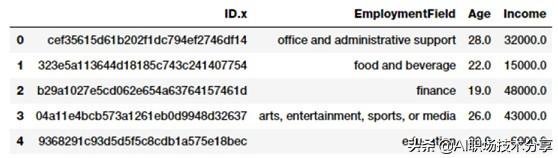
文章插图
来自FCC编码员调查数据集的样本属性对于每个参加调查的编码员或开发者， ID.x 变量基本上是一个唯一的标识符而其他字段是可自我解释的。
等宽分区间就像名字表明的那样，在等宽分区间方法中，每个区间都是固定宽度的，通常可以预先分析数据进行定义。基于一些领域知识、规则或约束，每个区间有个预先固定的值的范围，只有处于范围内的数值才被分配到该区间。基于数据舍入操作的分区间是一种方式，你可以使用数据舍入操作来对原始值进行分区间，我们前面已经讲过。