生活_傻大方

  1. 首页 > 潮·科技 > >

「排序」堆排序不难！看完这篇你也能手写堆排序啦( 二 )


堆排序上面的一个堆建造完毕之后 ， 我们怎么去利用这个堆实现排序呢？答案也是很简单的 ， 我们知道堆有一个特性就是堆顶是最小(或最大) ， 而我们建造这个如果去除第一个元素 ， 剩余左右孩子依然满足堆的性质 。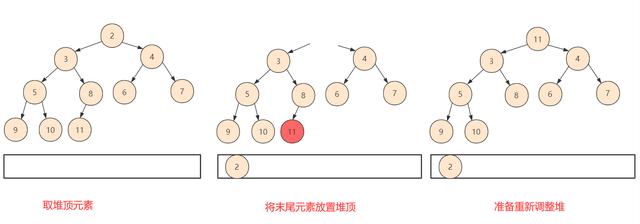
「排序」堆排序不难！看完这篇你也能手写堆排序啦文章插图
将最后一个元素放置堆顶 ， 由于第一个元素的存在使得整个不满足堆的性质 。 分析这个结构 ， 和我们前面构造堆的过程中构造到第一个元素的操作相同：

  • 判断左右孩子 ， 如果需要交换则交换 ， 交换后再次考虑交换子节点是否需要交换 。 一直到不需要考虑 。

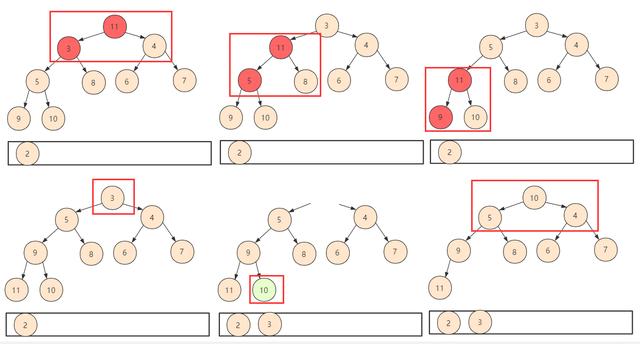「排序」堆排序不难！看完这篇你也能手写堆排序啦文章插图
这样到最后 ， 堆排序即可完成 ， 最终得到的序列即为堆排序序列 。
一个大根堆的排序过程如下：
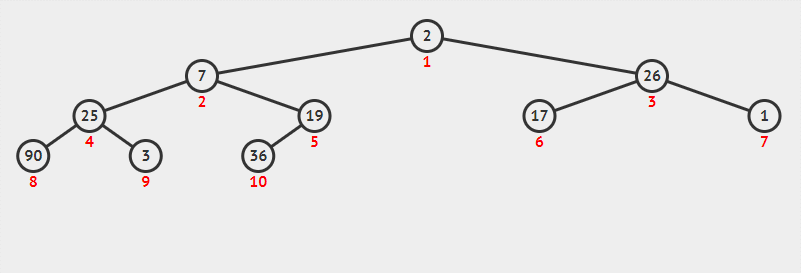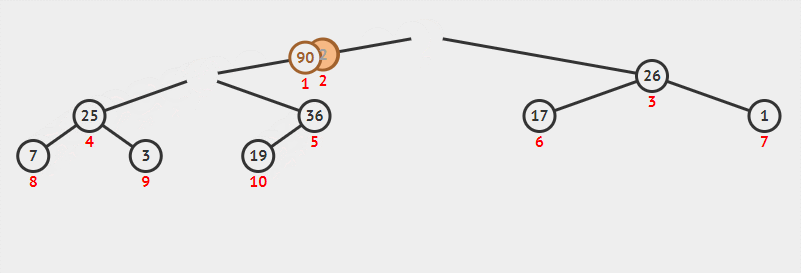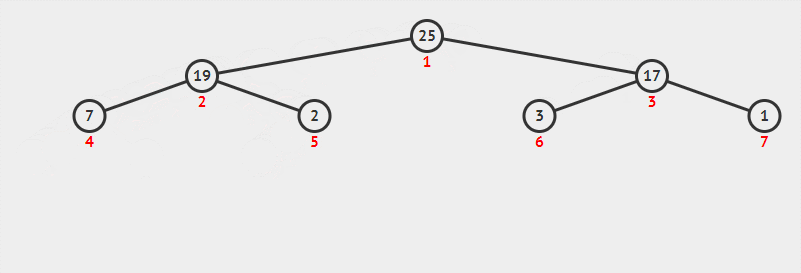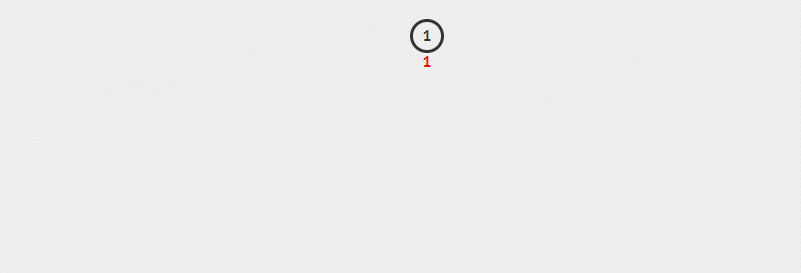「排序」堆排序不难！看完这篇你也能手写堆排序啦文章插图
具体实现有了上述的思想之后 ， 如何具体的实现这个堆排序的代码呢？从细致的流程来看 ， 大概流程是如下的：
给定数组建堆(creatHeap)
  • 从第一个非叶子节点开始判断交换下移(shiftDown) ， 使得当前节点和子孩子能够保持堆的性值
  • 如果交换打破子孩子堆结构性质 ， 那么就要重新下移(shiftDown)被交换的节点一直到停止 。
堆构造完成 ， 取第一个堆顶元素为最小(最大) ， 剩下左右孩子依然满足堆的性值 ， 但是缺个堆顶元素 ， 如果给孩子调上来 ， 可能会调动太多并且可能破坏堆结构 。
  • 所以索性把最后一个元素放到第一位 。 这样只需要判断交换下移(shiftDown）,不过需要注意此时整个堆的大小已经发生了变化 ， 我们在逻辑上不会使用被抛弃的位置 ， 所以在设计函数的时候需要附带一个堆大小的参数 。
  • 重复以上操作 ， 一直堆中所有元素都被取得停止 。
而堆算法复杂度的分析上 ， 之前建堆时间复杂度是O(n) 。 而每次删除堆顶然后需要向下交换 ， 每个个数最坏为logn个 。 这样复杂度就为O(nlogn).总的时间复杂度为O(n)+O(nlogn)=O(nlogn).
具体实现的代码如下：
import java.util.Arrays;public class 堆排序 {static void swap(int arr[],int m,int n){int team=arr[m];arr[m]=arr[n];arr[n]=team;}//下移交换 把当前节点有效变换成一个堆(小根)static void shiftDown(int arr[],int index,int len)//0 号位置不用{int leftchild=index*2+1;//左孩子int rightchild=index*2+2;//右孩子if(leftchild>=len)return;else if(rightchild执行结果：
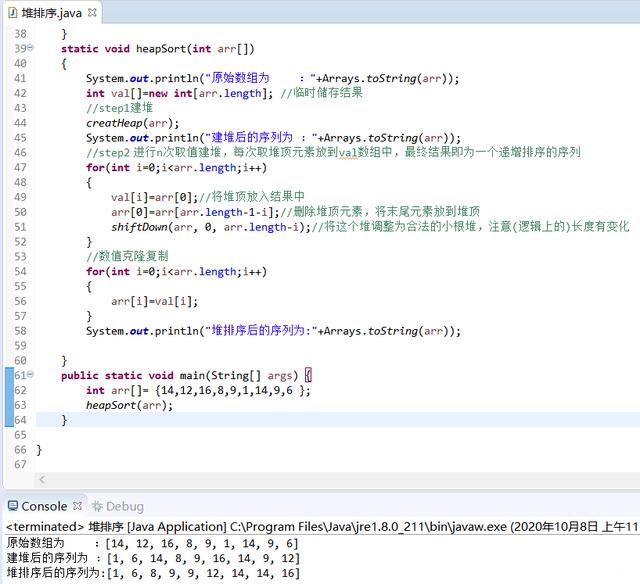「排序」堆排序不难！看完这篇你也能手写堆排序啦文章插图
当然 ， 代码为了成章节我把它命名为中文 ， 还有些不规范的地方请注意甄别 。
结语对于堆排序就先介绍到这里了 ， 当然堆的强大之处不止这么一点 ， 优先队列同样也是用到堆但是这里就不详细介绍了 ， 我相信优秀的你肯定又掌握了一门O(nlogn)级别的排序算法啦 。 如果写的有啥不确切地方还请指正 。
最后 ， 如果感觉不错一键三联哦！ ， 欢迎关注公众号：bigsai,更多精彩等你来看 。 期待你的关注 ， 并且笔者也准备了一波pdf学习资源分享给你 。
「排序」堆排序不难！看完这篇你也能手写堆排序啦文章插图



上一篇：卡西欧手电筒红外温度感应器——CASIO tsr100

下一篇：理性探讨：为什么国内LTE室内覆盖能力差？