「排序」堆排序不难！看完这篇你也能手写堆排序啦原创公众号：bigsai,码字不易

原创公众号：bigsai,码字不易，如有帮助，记得三联！
前言在个人的专栏中，其他排序陆陆续续都已经写了，而堆排序迟迟没有写，在国庆假期的尾声，把堆排序也写一写。
插入类排序—(折半)插入排序、希尔排序交换类排序—冒泡排序、快速排序手撕图解归并类排序—归并排序(逆序数问题)计数排序引发的围观风波——一种O(n)的排序两分钟搞懂桶排序
对于常见的快排、归并这些O(nlogn)的排序算法，我想大部分人可能很容易搞懂，但是堆排序大部分人可能比较陌生，或许在Java的comparator接口中可能了解一点。但堆排序在应用中比如优先队列此类维护动态数据效率比较高，有着非常广泛的应用。
而堆排序可以拆分成堆和排序，其中你可能对堆比较陌生，对排序比较熟悉，下面就带你彻底了解相关内容。
文章插图
堆什么是堆？
谈起堆，很多人第一联想到的是土堆，而在数据结构中这种土堆与完全二叉树更像，而堆就是一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树(完全)的数组对象。且总是满足以下规则：

堆总是一棵完全二叉树
每个节点总是大于(或小于)它的孩子节点。

完全二叉树我想什么是完全二叉树大部分人也是知道：最后一层以上都是满的，最后一层节点从左到右可以排列(有任何空缺即不满足完全二叉树) 。

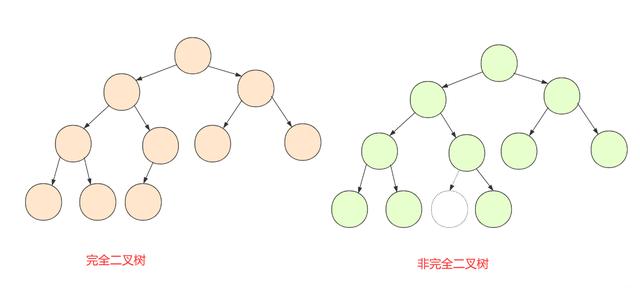文章插图
看作树的数组对象我们都知道我们排序的对象一般都是对数组之类的序列进行排序，如果转成抽象数据结构再实现可能成本比较大。
我们正常在构造一棵二叉树的时候通常采用链式left ， right节点，但其实二叉树的表示方式用数组也可以实现，只不过普通的二叉树如果用数组储存可能空间利用效率会很低而很少采用，但我们的堆是一颗完全二叉树。使用数组储存空间使用效率也比较高，所以在形式上我们把这个数组看成对应的完全二叉树，而操作上可以直接操作数组也比较方便。

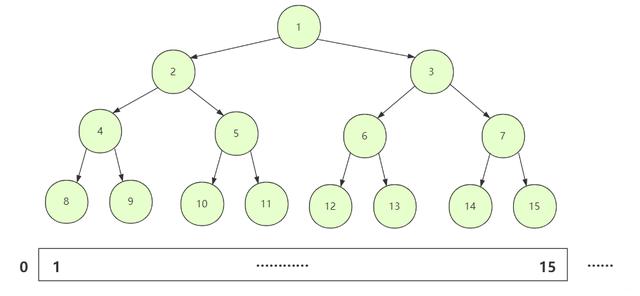文章插图
大根堆 VS 小根堆上面还有一点就是在这个完全二叉树中所有节点均大于(或小于)它的孩子节点，所以这里就分为两种情况

如果所有节点大于孩子节点值，那么这个堆叫做大根堆，堆的最大值在根节点。
如果所有节点小于孩子节点值，那么这个堆叫做小根堆，堆的最小值在根节点。

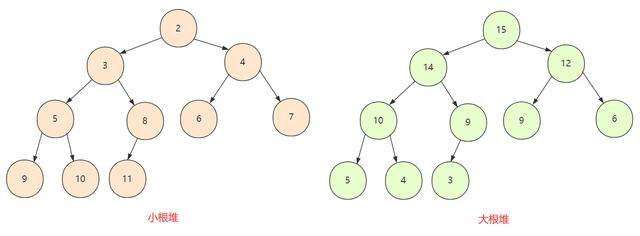文章插图
堆排序【「排序」堆排序不难！看完这篇你也能手写堆排序啦】通过上面的介绍，我想你对堆应该有了一定的认识，堆排序肯定是借助堆实现的某种排序，其实堆排序的整体思路也很简单，就是

构建堆，取堆顶为最小(最大) 。
将剩下的元素重新构建一个堆，取堆顶，一直到元素取完为止。

建堆如果给一个无序的序列，首先要给它建成一个堆，我们如何实现这个操作呢？以下拿一个小根堆为例进行分析。
对于二叉树(数组表示) ，我们从下往上进行调整，从第一个非叶子节点开始向前调整，对于调整的规则如下：
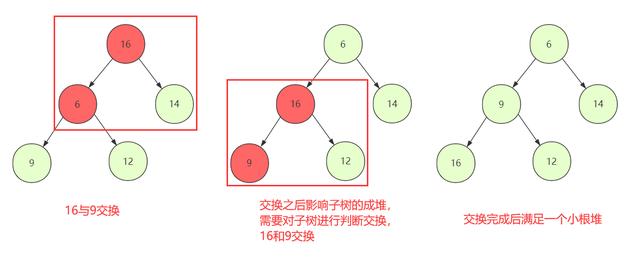
①对于小根堆，当前节点与左右孩子比较，如果均小于左右孩子节点，那么它本身就是一个小根堆，它不需要做任何改变，如果左右有孩子节点比它还小，那么就要和最小的那个进行替换。

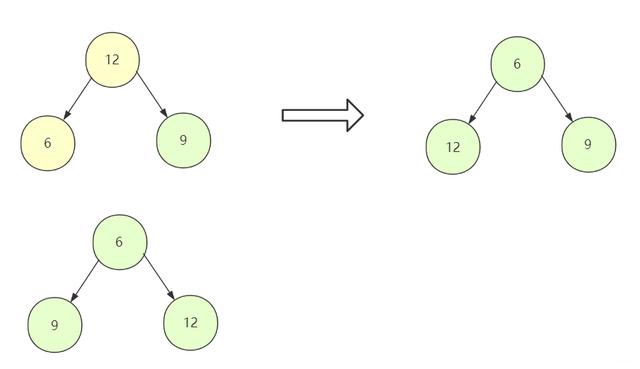文章插图
②但是普通节点替换可能没问题，对于某些和子节点替换有可能改变子树成堆，所以需要继续往下判断交换(最差判断到叶子节点) 。

文章插图
分析构造堆的这个过程，每个非叶子节点都需要判断比较是否交换，这样一层就是O(n) ，而每个节点可能替换之后影响子节点成堆需要再往下判断遍历，你可能会认为它是一个O(nlogn),但其实你看看二叉树性值，大部分都是在底部的，上面的只有很少个数，如果你用数学方法去求得最终的复杂度它还是一个O(n)级别，这里就不作详细介绍了。
一个大根堆建立过程也是一样的：

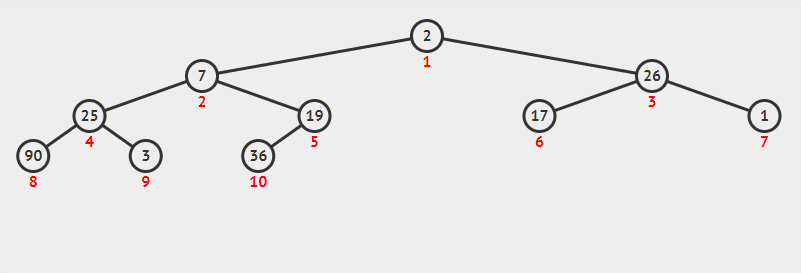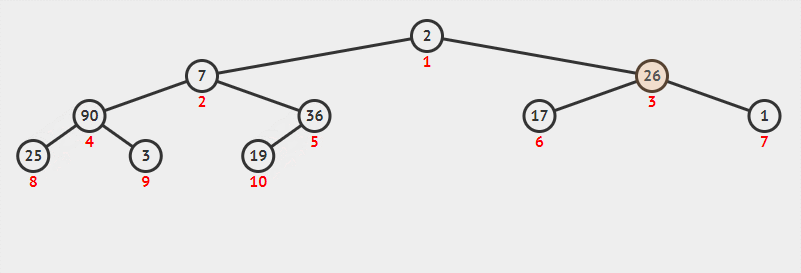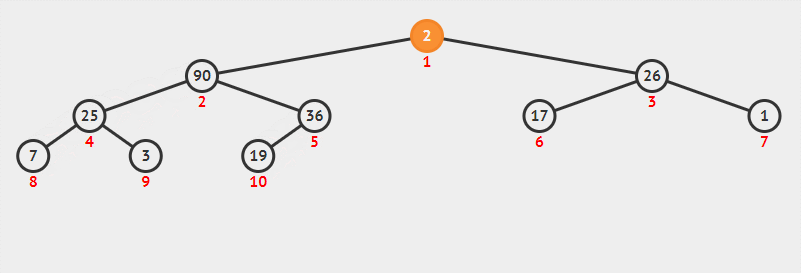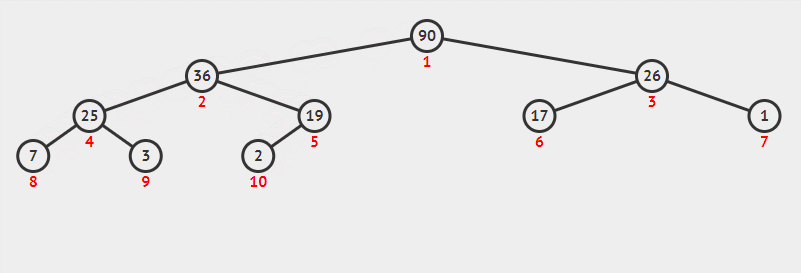文章插图