现在我们要需要考虑一下这样的一颗语法树如何做召回 。 一种很直观的做法是这样的：
1 节点6与节点7的倒排链进行求交 ， 得到的pageid作为节点4的pageid2 节点2的pageid = min(节点4 pageid ， 节点5 pageid)3 比较节点2的pageid与节点3的pageid3.1 节点2 pageid = 节点3 pageid则弹出该节点作为求交结果 ， 所有节点对应的倒排链后移一位3.2 节点2 pageid < 节点3 pageid节点2先内部求交得到一个大于等于节点3 pageid的文档3.3 节点2 pageid > 节点3 pageid节点3对应的倒排链查找第一个大于等于节点2 pageid的文档上述过程一直持续有节点2或者节点3有节点到达了末尾为止 。 其中节点2由于是一颗子树 ， 它是否到达末尾 ， 由其子节点节点4与节点5到达了末尾为止 ， 节点4同理 。 关于pageid在建索引库时我们会对进入到该索引库的文档按L0得分排序 ， 从0开始重新编号 ， 当然库内会有一片区域保存库内pageid到原docid的映射关系 。 这一点的主要目的是为了保证倒排链中的文档按L0得分排列后依然有序 ， 次要目的是为了对倒排链进行压缩 。 但是对于内存搜索引擎而言 ， 我们暂时还没有尝试对倒排链进行压缩 ， 一方面是因为CPU同样是紧张资源 ， 另一方面团队也还没有精力投入到这一块 。 因此目前其最大的作用只是保证了倒排链中的文档id有序 ， 以及库内文档id的连续(从而可以根据库内文档id直接下标访问文档数据) ， 另外把8字节的文档id ， 转成了4字节的库内pageid ， 省了一半内存 。 本人之前听到过多次这样的说法：语法树的层级越高 ， 求交的性能就会越差 。 如果是按照我上面所述的求交方式的话 ， 那么的确是的 ， 层级越高 ， 求交性能就会越差 。 原因是什么呢？
原因在于高层级的语法树进行求交时可能会存在一些不必要的求交行为 。 以上面的那颗 3 层语法树为例 ， 假如节点 6[苹果]和节点 7[手机]这两条倒排链中的 pageid 都非常小 ， 而节点 3 的 pageid 比较大时 ， 那么有可能节点 2 所有的求交结果都来自节点 5 。
那为什么会存在一些不必要的求交行为呢？其本质在于上面所述的求交方式是一种逻辑先验的求交算法 。 下面介绍一种逻辑后验的算法 。
定义求交基准为一个可能的求交结果1 计算求交基准N = max( min( max(节点6 pageid, 节点7 pageid), 节点5 pageid), 节点3 pageid)2 所以倒排链全部往N靠拢 ， 找到第一个>=N的位置3 判断所有倒排链当前的结果是否符合求交逻辑关系 ， 若符合则弹出结果且相关节点后移一位 。 4 判断是否求交结束 ， 如果未结束则流程回到1 ， 否则退出求交损耗的本质为各条倒排链的跳跃查找次数 ， and/or 等语法只是建立在倒排链的跳跃查找之上的逻辑关系 ， 跳跃查找次数越少的 ， 性能也就越好 。 在逻辑后验求交算法里 ， 每次选出的求交基准 N 都是一个可能的求交结果 ， 也就是说除非我们能找到新的算法可以再次排除一些可能的求交结果位置 ， 否则不会有比它性能更好的语法树求交算法 。
现在尝试一下将语法树打平 ， 看一下打平后的语法树具备哪些方面的优势 。 这里要介绍的是我们上一代内存搜索引擎中将 3 层结构语法树转化为 2 层结构语法树进行求交的做法 。
笛卡尔积语法树通过将 3 层语法树结构里的同义词节点做笛卡尔积 ， 可得到与其等效的 2 层结构语法树 ， 还是以 query [苹果手机回收] 为例 ， 其中 [苹果手机]和[iphone] 互为同义词,将其转换为笛卡尔积语法树后 ， 其结构如下图所示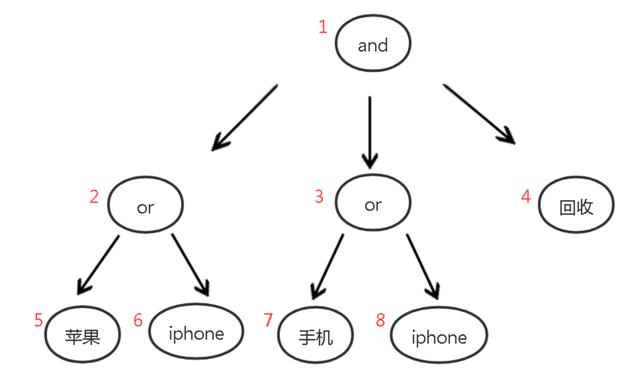
文章插图
其原理为(A--tt-darkmode-color: #8F9BAB;">当然这里的同义词组更简单 ， 为(A--tt-darkmode-color: #8F9BAB;">为了能够更具体一点的了解不同语法树之间的性能差异 。 我们需要对求交性能做一个定量的分析 。 下面对 3 层结构的原语法树和其对应的笛卡尔积语法树各自的求交过程来进行性能分析 ， 依然以苹果手机回收这个 case 为例 。
1 原语法树求交基准的计算公式:(此处直接以Term值来表示对应Term节点)max ( min(苹果--tt-darkmode-color: #8F9BAB;">为了简化性能评估 ， 我们假定每次语法节点的操作损耗相同 ， 则性能评估的大致公式为:
文章插图
从公式上来看 ， 决定性能的因素主要有以下 4 点：


• 求交基准总数
• 语法节点个数
• 求交基准选取损耗
• 语法树节点操作个数