本文的代码 github/fkodom/fft-conv-pytorch
附录卷积与互相关
在本文前面 ， 我们通过在傅立叶空间中获取内核的复共轭来实现互相关 。这有效地扭转了内核的方向 ， 现在我想证明为什么 。首先 ， 请记住卷积和互相关的公式：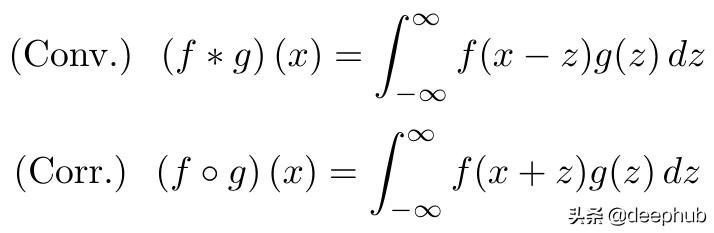
文章插图
然后 ， 让我们看一下内核的傅里叶变换（g）：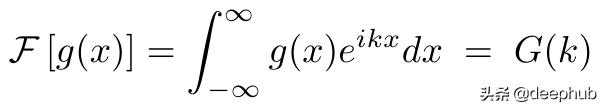
文章插图
取G的复共轭 。 请注意 ， 内核g（x）是实值 ， 因此不受共轭影响 。然后 ， 更改变量（y = -x）并简化表达式 。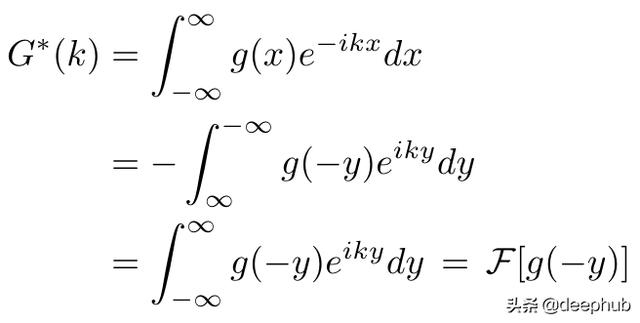
文章插图
因此 ， 我们有效地改变了内核的方向！
作者 Frank Odom
【PyTorch中傅立叶卷积：计算大核卷积的数学原理和代码实现】deephub翻译组

• 在Linux系统中安装深度学习框架Pytorch
• 输出层|PyTorch可视化理解卷积神经网络
• 类别|如何用PyTorch进行语义分割？一个教程教会你
• PyTorch1.7发布，支持CUDA11分布式训练
• 在TPU上运行PyTorch的技巧总结
• 如何在PyTorch和TensorFlow中训练图像分类模型
• 如何利用PyTorch中的Moco-V2减少计算约束
• 检测器|案例解析：用Tensorflow和Pytorch计算骰子值
• 将PyTorch投入生产的5个常见错误
• 使用PolyGen和PyTorch生成3D模型