PyTorch中傅立叶卷积：计算大核卷积的数学原理和代码实现( 二 ) 卷积卷积在数据分析中无处不

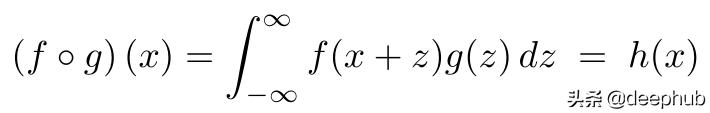文章插图
与卷积相比，这有效地逆转了核函数(g)的方向。我们不是手动翻转核函数，而是通过求傅里叶空间中核函数的复共轭来修正。因为我们不需要创建一个全新的张量，所以这大大加快了存储效率。 (本文末尾的附录中包含了如何/为什么这样做的简要演示。 )
# 3. Multiply the transformed matricesdef complex_matmul(a: Tensor, b: Tensor) -> Tensor:"""Multiplies two complex-valued tensors."""# Scalar matrix multiplication of two tensors, over only the first two dimensions.# Dimensions 3 and higher will have the same shape after multiplication.scalar_matmul = partial(torch.einsum, "ab..., cb... -> ac...")# Compute the real and imaginary parts independently, then manually insert them# into the output Tensor.This is fairly hacky but necessary for PyTorch 1.7.0,# because Autograd is not enabled for complex matrix operations yet.Not exactly# idiomatic PyTorch code, but it should work for all future versions (>= 1.7.0).real = scalar_matmul(a.real, b.real) - scalar_matmul(a.imag, b.imag)imag = scalar_matmul(a.imag, b.real) + scalar_matmul(a.real, b.imag)c = torch.zeros(real.shape, dtype=torch.complex64)c.real, c.imag = real, imagreturn c# Conjugate the kernel for cross-correlationkernel_fr.imag *= -1output_fr = complex_matmul(signal_fr, kernel_fr)PyTorch 1.7改进了对复数的支持，但是autograd中还不支持对复数值张量的许多操作。现在，我们必须编写自己的complex_matmul方法作为补丁。虽然不是最佳的解决方案，但它目前可以工作。
4 计算逆变换
使用torch.irfftn可以很容易地计算出逆变换。然后，裁剪出多余的数组填充。
# 4. Compute inverse FFT, and remove extra padded valuesoutput = irfftn(output_fr, dim=-1)output = output[:, :, :signal.size(-1) - kernel.size(-1) + 1]5 添加偏置并返回
添加偏置项也非常容易。请记住，偏置对输出阵列中的每个通道都有一个元素，并进行相应的整形。
# 5. Optionally, add a bias term before returning.if bias is not None:output += bias.view(1, -1, 1)放在一起
为了完整起见，让我们将所有这些代码段编译为一个内聚函数。
def fft_conv_1d(signal: Tensor, kernel: Tensor, bias: Tensor = None, padding: int = 0,) -> Tensor:"""Args:signal: (Tensor) Input tensor to be convolved with the kernel.kernel: (Tensor) Convolution kernel.bias: (Optional, Tensor) Bias tensor to add to the output.padding: (int) Number of zero samples to pad the input on the last dimension.Returns:(Tensor) Convolved tensor"""# 1. Pad the input signal & kernel tensorssignal = f.pad(signal, [padding, padding])kernel_padding = [0, signal.size(-1) - kernel.size(-1)]padded_kernel = f.pad(kernel, kernel_padding)# 2. Perform fourier convolutionsignal_fr = rfftn(signal, dim=-1)kernel_fr = rfftn(padded_kernel, dim=-1)# 3. Multiply the transformed matriceskernel_fr.imag *= -1output_fr = complex_matmul(signal_fr, kernel_fr)# 4. Compute inverse FFT, and remove extra padded valuesoutput = irfftn(output_fr, dim=-1)output = output[:, :, :signal.size(-1) - kernel.size(-1) + 1]# 5. Optionally, add a bias term before returning.if bias is not None:output += bias.view(1, -1, 1)return output测试最后，我们将确认这在数值上等于使用torch.nn.functional.conv1d进行直接一维卷积。我们为所有输入构造随机张量，并测量输出值的相对差异。
import torchimport torch.nn.functional as ftorch.manual_seed(1234)kernel = torch.randn(2, 3, 1025)signal = torch.randn(3, 3, 4096)bias = torch.randn(2)y0 = f.conv1d(signal, kernel, bias=bias, padding=512)y1 = fft_conv_1d(signal, kernel, bias=bias, padding=512)abs_error = torch.abs(y0 - y1)print(f'\nAbs Error Mean: {abs_error.mean():.3E}')print(f'Abs Error Std Dev: {abs_error.std():.3E}')# Abs Error Mean: 1.272E-05# Abs Error Std Dev: 9.937E-06每个元素相差约1e-5-相当准确，考虑到我们使用的是32位精度！我们还可以执行一个快速基准测试来衡量每种方法的速度：
from timeit import timeitdirect_time = timeit("f.conv1d(signal, kernel, bias=bias, padding=512)",globals=locals(),number=100) / 100fourier_time = timeit("fft_conv_1d(signal, kernel, bias=bias, padding=512)",globals=locals(),number=100) / 100print(f"Direct time: {direct_time:.3E} s")print(f"Fourier time: {fourier_time:.3E} s")# Direct time: 1.523E-02 s# Fourier time: 1.149E-03 s所测得的基准将随着您所使用的机器而发生重大变化。（我正在使用非常老的Macbook Pro进行测试。）对于1025的内核大小，傅立叶卷积似乎要快10倍以上。
总结本片文章对傅立叶卷积提供了详尽的介绍。我认为这是一个很酷的技巧，并且可以在许多实际应用中使用它。我也很喜欢数学，因此很高兴看到编程和纯数学的这种交汇。欢迎并鼓励所有评论和建设性批评。