文章插图
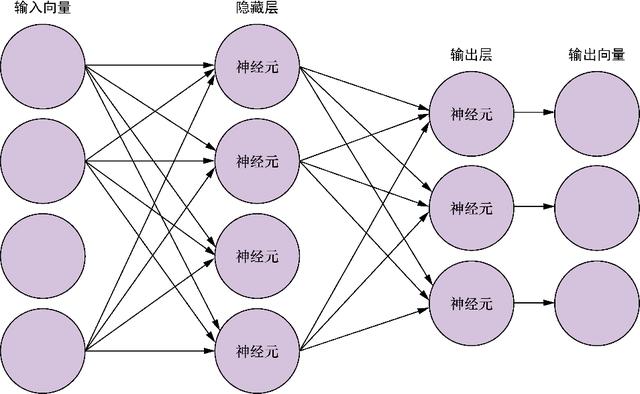
图5-7　全连接神经网络
到目前为止 ， 大家一直在使用阶跃函数作为人工神经元的激活函数 。 但是接下来会发现 ， 反向传播需要一个非线性连续可微的激活函数[11] ， 如公式5-4中常用的sigmoid函数所示 ， 现在每个神经元都会输出介于两个值（如0和1）之间的值：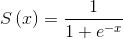
文章插图
公式5-4　sigmoid函数
为什么激活函数需是非线性的
因为需要让神经元能够模拟特征向量和目标变量之间的非线性关系 。 如果神经元只是将输入与权重相乘然后做加和 ， 那么输出必然是输入的线性函数 ， 这个模型连最简单的非线性关系都无法表示 。
之前使用的神经元阈值函数是一个非线性阶跃函数 。 所以理论上只要有足够多的神经元就可以用来训练非线性关系模型 。
这就是非线性激活函数的优势 ， 它使神经网络可以建立非线性关系模型 。 一个连续可微的非线性函数 ， 如sigmoid ， 可以将误差平滑地反向传播到多层神经元上 ， 从而加速训练进程 。 sigmoid神经元的学习速度很快 。
还有许多其他的激活函数 ， 如双曲正切函数和修正线性单元函数 ， 它们各有优劣 ， 适用于不同的神经网络结构 ， 大家将在之后的章节中学习 。
为什么要求可微呢？如果能够计算出这个函数的导数 ， 就能对函数中的各个变量求偏导数 。 这里的关键是“各个变量” ， 这样就能通过接收到的输入来更新权重！
7．求导首先用平方误差作为代价函数来计算网络的误差 ， 如公式5-5所示[12]：
文章插图
公式5-5　均方误差
然后利用微积分链式法则计算复合函数的导数 ， 如公式5-6所示 。 网络本身只不过是函数的复合（点积之后的非线性激活函数） 。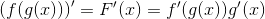
文章插图
公式5-6　链式法则
接下来可以用这个公式计算每个神经元上激活函数的导数 。 通过这个方法可以计算出各个权重对最终误差的贡献 ， 从而进行适当的调整 。
如果该层是输出层 ， 借助于可微的激活函数 ， 权重的更新比较简单 ， 对于第j个输出 ， 误差的导数如下[13]：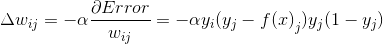
文章插图
公式5-7　误差导数
如果要更新隐藏层的权重 ， 则会稍微复杂一点儿 ， 如公式5-8所示：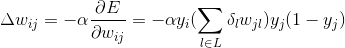
文章插图
公式5-8　前一层的导数
在公式5-7中 ， 函数f(x)表示实际结果向量 ， f(x)j表示该向量第j个位置上的值 ， yi、yj是倒数第二层第i个节点和输出第j个节点的输出 ， 连接这两个节点的权重为wij ， 误差代价函数对wij求导的结果相当于用α（学习率）乘以前一层的输出再乘以后一层代价函数的导数 。 公式5-8中δl表示L层第l个节点上的误差项 ， 前一层第j个节点到L层所有的节点进行加权求和[14] 。
重要的是要明确何时更新权重 。 在计算每一层中权重的更新时 ， 需要依赖网络在前向传播中的当前状态 。 一旦计算出误差 ， 我们就可以得到网络中各个权重的更新值 ， 但仍然需要回到网络的起始节点才能去做更新 。 否则 ， 如果在网络末端更新权重 ， 前面计算的导数将不再是对于本输入的正确的梯度 。 另外 ， 也可以将权重在每个训练样本上的变化值记录下来 ， 其间不做任何更新 ， 等训练结束后再一起更新 ， 我们将在5.1.6节中讨论这项内容 。
接下来将全部数据输入网络中进行训练 ， 得到每个输入对应的误差 ， 然后将这些误差反向传播至每个权重 ， 根据误差的总体变化来更新每个权重 。 当网络处理完全部的训练数据后 ， 误差的反向传播也随之完成 ， 我们将这个过程称为神经网络的一个训练周期（epoch） 。 我们可以将数据集一遍又一遍地输入网络来优化权重 。 但是要注意 ， 网络可能会对训练集过拟合 ， 导致对训练集外部的新数据无法做出有效的预测 。
在公式5-7和公式5-8中 ， α表示学习率 。 它决定了在一个训练周期或一批数据中权重中误差的修正量 。 通常在一个训练周期内α