有关自然语言处理的深度学习知识有哪些？( 五 ) .font_s.ios.pgcarticle

接下来我们暂停一下，将这个过程的一个重要部分形式化。到目前为止，我们已经讨论了误差和感知机的预测结果与真实结果的偏离程度。测量这个误差是由代价函数或损失函数来完成的。正如我们看到的，代价函数量化了对于输入“问题”（x）网络应该输出的正确答案与实际输出值（y）之间的差距。损失函数则表示网络输出错误答案的次数以及错误总量。公式5-2是代价函数的一个例子，表示真实值与模型预测值之间的误差：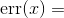
文章插图
公式5-2　真实值与预测值之间的误差
训练感知机或者神经网络的目标是最小化所有输入样本数据的代价函数。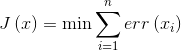
文章插图
公式5-3　希望最小化的代价函数
接下来大家会看到还有一些其他种类的代价函数，如均方误差，这些通常已经在神经网络框架中定义好了，大家无须自己去决定哪些是最好的代价函数。需要牢记的是，最终目标是将数据集上的代价函数最小化，这样此处给出的其他概念才有意义。
6．反向传播算法辛顿（Hinton）和他的同事提出一种用多层感知机同时处理一个目标的方法。这个方法可以解决线性不可分问题。通过该方法，他们可以像拟合线性函数那样去拟合非线性函数。
但是如何更新这些不同感知机的权重呢？造成误差的原因是什么？假设两个感知机彼此相邻，并接收相同的输入，无论怎样处理输出（连接、求和、相乘），当我们试图将误差传播回到初始权重的时候，它们（输出）都将是输入的函数（两边是相同的），所以它们每一步的更新量都是一样的，感知机不会有不同的结果。这里的多个感知机将是冗余的。它们的权重一样，神经网络也不会学到更多东西。
大家再来想象一下，如果将一个感知机作为第二个感知机的输入，是不是更令人困惑了，这到底是在做什么？
反向传播可以解决这个问题，但首先需要稍微调整一下感知机。记住，权重是根据它们对整体误差的贡献来更新的。但是如果权重对应的输出成为另一个感知机的输入，那么从第二个感知机开始，我们对误差的认识就变得有些模糊了。
如图5-6所示，权重w1i通过下一层的权重（w1j）和（w2j）来影响误差，因此我们需要一种方法来计算w1i对误差的贡献，这个方法就是反向传播。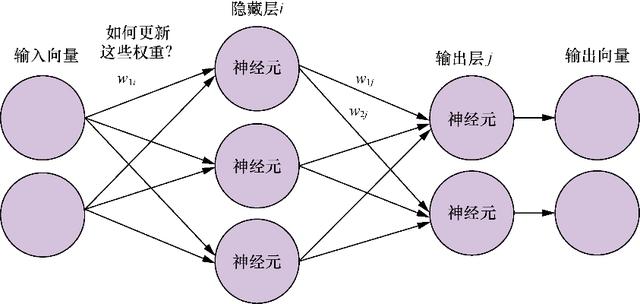
文章插图
图5-6　包含隐藏权重的神经网络
现在是时候停止使用“感知机”这个术语了，因为之后大家将改变每个神经元权重的更新方式。从这里开始，我们提到的神经元将更通用也更强大，它包含了感知机。在很多文献中神经元也被称为单元或节点，在大多数情况下，这些术语是可以互换的。
所有类型的神经网络都是由一组神经元和神经元之间的连接组成的。我们经常把它们组织成层级结构，不过这不是必需的。如果在神经网络的结构中，将一个神经元的输出作为另一个神经元的输入，就意味着出现了隐藏神经元或者隐藏层，而不再只是单纯的输入层、输出层。
图5-7中展示的是一个全连接网络，图中没有展示出所有的连接，在全连接网络中，每个输入元素都与下一层的各个神经元相连，每个连接都有相应的权重。因此，在一个以四维向量为输入、有5个神经元的全连接神经网络中，一共有20个权重（5个神经元各连接4个权重）。
感知机的每个输入都有一个权重，第二层神经元的权重不是分配给原始输入的，而是分配给来自第一层的各个输出。从这里我们可以看到计算第一层权重对总体误差的影响的难度。第一层权重对误差的影响并不是只来自某个单独权重，而是通过下一层中每个神经元的权重来产生的。虽然反向传播算法本身的推导和数学细节非常有趣，但超出了本书的范围，我们对此只做一个简单的概述，使大家不至于对神经网络这个黑盒一无所知。
反向传播是误差反向传播的缩写，描述了如何根据输入、输出和期望值来更新权重。传播，或者说前向传播，是指输入数据通过网络“向前”流动，并以此计算出输入对应的输出。要进行反向传播，首先需要将感知机的激活函数更改为稍微复杂一点儿的函数。