有关自然语言处理的深度学习知识有哪些？( 四 ) .font_s.ios.pgcarticle

4．下一步基本感知机有一个固有缺陷，那就是，如果数据不是线性可分的，或者数据之间的关系不能用线性关系来描述，模型将无法收敛，也将不具有任何有效预测的能力，因为它无法准确地预测目标变量。
早期的实验在仅基于样本图像及其类别来进行图像分类的学习上取得了成功。这个概念在早期很激动人心，但很快受到了来自明斯基（Minsky）和佩珀特（Papert）的考验[6] ，他们指出感知机在分类方面有严重的局限性，他们证明了如果数据样本不能线性可分为独立的组，那么感知机将无法学习如何对输入数据进行分类。
线性可分的数据点（如图5-4所示）对感知机来说是没有问题的，而存在类别交叉的数据将导致单神经元感知机原地踏步，学习预测的结果将不比随机猜测好，表现得就像是在随机抛硬币。在图5-5中我们就无法在两个类（分别用点和叉表示）之间画一条分割线。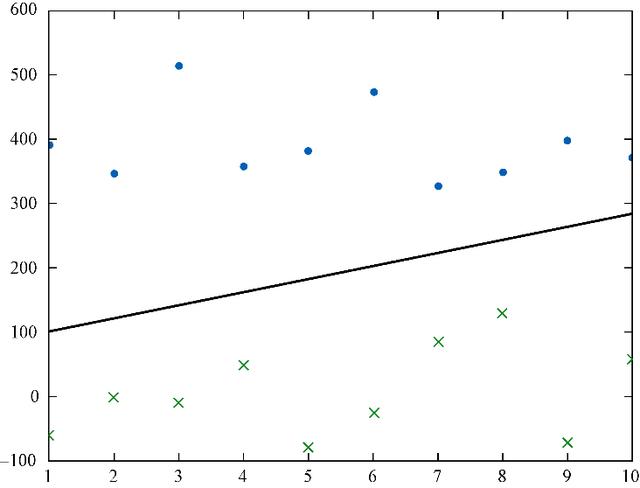
文章插图
图5-4　线性可分的数据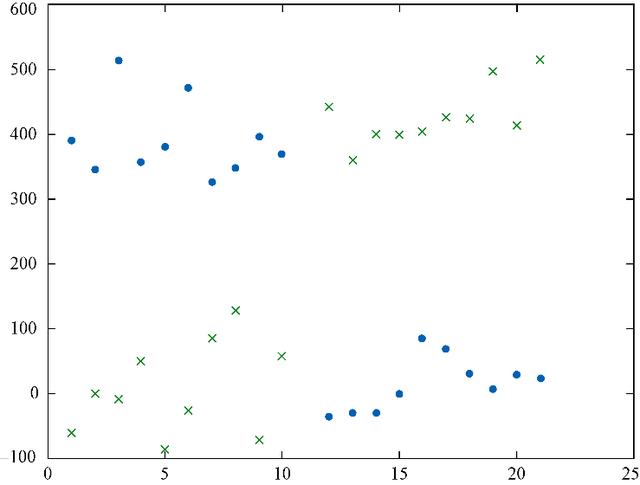
文章插图
图5-5　非线性可分的数据
感知机会用线性方程来描述数据集的特征与数据集中的目标变量之间的关系，这就是线性回归，但是感知机无法描述非线性方程或者非线性关系。
局部极小值与全局极小值
当一个感知机收敛时，可以说它找到了一个描述数据与目标变量之间关系的线性方程。然而，这并不能说明这个描述性线性方程有多好，或者说代价有多“小” 。如果有多个解决方案，即存在着多个可能的极小代价，它只会确定一个由权重初始值决定的、特定的极小值。这被称为局部极小值，因为它是在权重开始的地方附近找到的最优值（最小的代价）。它可能不是全局极小值，因为全局极小值需要搜索所有可能的权重值。在大多数情况下，无法确定是否找到了全局极小值。
很多数据值之间的关系不是线性的，也没有好的线性回归或线性方程能够描述这些关系。许多数据集不能用直线或平面来线性分割。因为世界上的大多数数据不能由直线或平面来清楚地分开，明斯基和佩珀特发表的“证明”让感知机被束之高阁。
但是有关感知机的想法并不会就此消亡。 Rumelhardt McClelland的合作成果[7]（Geoffrey Hinton也参与其中）展示了可以使用多层感知机的组合来解决异或（XOR）问题[8] ，此后感知机再次浮出水面。之前，大家使用单层感知机解决的或（OR）问题属于比较简单的问题，也没有用到多层反向传播。 Rumelhardt McClelland的关键突破是发现了一种方法，该方法可以为每个感知机适当地分配误差。他们使用的是一种叫反向传播的传统思想，通过这种跨越多个神经元层的反向传播思想，第一个现代神经网络诞生了。
基本感知机有一个固有的缺陷，即如果数据不是线性可分的，则模型不会收敛到具有有效预测能力的解。
注意
代码清单5-3中的代码通过一个单层感知机解决了或问题。代码清单5-1代码中感知机学到的0和1组成的表格是二元逻辑或的输出结果。异或问题稍微改变了一下该数据表，以此来教感知机如何模拟一个独占的逻辑或门。如果改变一下最后一个示例的正确结果，将1（真）改为0（假），从而将其转换为逻辑异或，这个问题就会变得困难许多。在不向神经网络添加额外神经元的情况下，每类（0或1）样本将是非线性可分的。在二维特征向量空间中，这些类彼此呈对角线分布（类似于图5-5），所以无法通过画一条直线来区分出数据样本1（逻辑真）和0（逻辑假）。
尽管神经网络可以解决复杂的非线性问题，但是那时计算成本太高，用两个感知机和一堆花哨的反向传播数学算法来解决异或问题被认为是对宝贵计算资源的极大浪费，因为这个问题只需要用一个逻辑门或一行代码就能解决。事实证明，它们不适合被广泛使用，所以只能再次回到学术界和超级计算机实验的角落。由此开启了第二次“人工智能寒冬” ，这种情况从1990年持续到2010年左右[9] 。后来，随着计算能力、反向传播算法和原始数据（例如猫和狗的标注图像[10]）的发展，昂贵的计算算法和有限的数据集都不再是障碍。第三次神经网络时代开始了。
下面我们来看看他们发现了什么。
5．第二次人工智能寒冬的出现和大多数伟大的思想一样，好的思想最终都会浮出水面。人们发现只要对感知机背后的基本思想进行扩展，就可以克服之前的那些限制。将多个感知机集合到一起，并将数据输入一个（或多个）感知机中，并且以这些感知机的输出作为输入，传递到更多的感知机，最后将输出与期望值进行比较，这个系统（神经网络）便可以学习更复杂的模式，克服了类的线性不可分的挑战，如异或问题。其中的关键是：如何更新前面各层中的权重？