按关键词阅读:
文章插图
编辑 | 维克多
好消息是,另一项研究发现对于三次多项式下的优化问题,存在快速求解的方法。具体而言,可以通过使用平方和检验(sum-of-squares test)找到某些多项式的最低点,进而搜索三次函数的局部最优解。
两项研究时隔两天,出自于同一研究团队:普林斯顿大学的Amir Ali Ahmadi和他的前学生Jeffrey Zhang。

文章插图

文章插图
论文1:On the complexity of finding a local minimizer of a quadratic function over a polytope
贡献:判定二次函数在(无界)多胞形( polyhedron)上是否有局极小值,以及判定四次多项式是否有局部极小值属于NP难。
论文链接:https://arxiv.org/abs/2008.05558
论文2:Complexity aspects of local minima and related notions
贡献:证明了在三次多项式中,某些优化问题容易处理,且给出了寻找三次多项式局部极小值的一个充要条件。
论文链接:https://arxiv.org/abs/2008.06148
这两篇论文,一前一后,证明了复杂性计算研究的现状:某种类型的优化问题很容易解决,而某种类型的问题则必然很难解决。更进一步,他们为从金融到自动系统等各个领域的优化问题确定了新的边界。
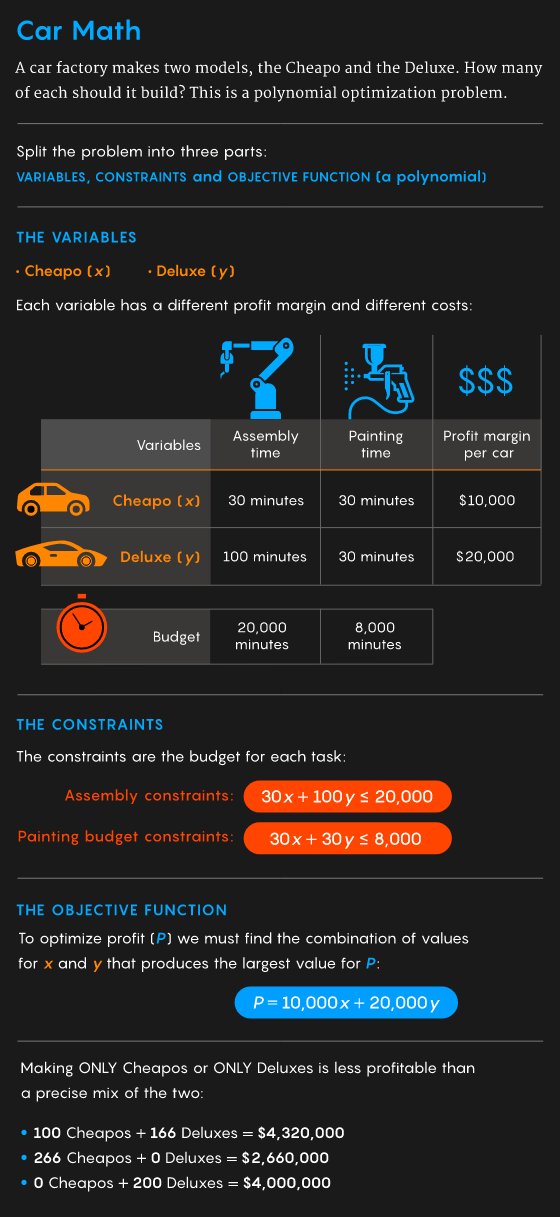
这个问题可以转化为一个用多项式表达的优化求解问题。
首先,这个问题可以分解为三个元素:
- 有待优化的可量化变量,比如必须生产的汽车数量。
- 一些约束条件,比如预算和生产能力。
- 一个叫做目标函数的东西,目标函数的功能是给定决策变量,输出解决方案(优化值)。
文章插图
汽车例子仅仅是一个简单的优化问题,变量之间没有相互作用,优化值可以通过求解线性函数得到。但现实中的问题往往非常复杂。
例如,如何选择最佳航空枢纽。枢纽航班波强度和密度的经济性与机场设备设施、机型、航班结构等等有关,只有在这几个方面取得最佳配合的情况下,枢纽中转才能真正发挥作用。
枢纽航空公司在组织航班的时候,希望航班波的强度和密度越大越好,这样就可以提高单位时间内的中转效率,与此带来的单位时间内航班量过大,中转人数过多的高峰处理量,给机场和航空公司带来了巨大的运营压力和成本压力。也就是说,航空公司在枢纽机场的处理能力接近峰值后,会出现快速衰退,导致操作成本快速提高和服务质量急剧下降。
当然,还有很多问题可能比这更复杂。变量之间的三阶交互作用需要用到更复杂的函数。每一步函数复杂性都要为更广泛的问题建模,但是这种复杂性是有代价的,它可能计算不出最优解。

稿源:(雷峰网)
【傻大方】网址:/c/1125a51532021.html
标题:复杂性|普林斯顿研究“最小值”:平方和的破局,二次和三次优化问题的极限