HybridPose：混合表示下的6D对象姿态估计( 二 ) 作者：康斯坦奇来源：公众号

2.3 位姿回归HybridPose的第二个模块将预测的中间表示{K ， E ， S}作为输入，并为输入图像I输出6D对象姿态RI∈SO（3）， tI∈R3 。类似于最新的姿态回归方法， HybridPose结合了初始化子模块和优化子模块。两个子模块均利用所有预测元素。优化子模块还利用强大的功能来对预测元素中的异常值进行建模。
在下文中，本文将规范坐标系中的3D关键点坐标表示为pk ， 1≤k≤| K | 。为了使符号整洁，本文将第一个模块的输出表示为，即预测的关键点，边缘向量和对称对应关系为pk∈R2,1≤k≤| K | ， ve∈R2,1≤e≤| E | ，和（qs ， 1∈R2 ， qs ， 2∈R2）， 1≤s≤| S | 。本文的公式还分别使用了pk ， ve ， qs ， 1和qs ， 2的齐次坐标? pk∈R3 ， ? ve∈R3 ， ? qs ， 1∈R3和? qs ， 2∈R3 。均质坐标由相机固有矩阵标准化。
初始化子模块。该子模块利用了RI ， tI和预测元素之间的约束，并在细微空间中求解Ri ， tI ，然后以交替优化的方式将其投影到SE（3）。为此，本文为每种类型的预测元素引入以下差异向量：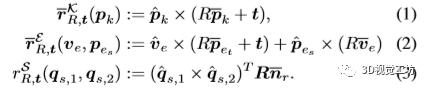
文章插图
其中es和et是边e的端点， ve = pet-pes∈R3 ，而nr∈R3是规范系统中反射对称平面的法线。
HybridPose修改了EPnP的框架以生成初始位姿。通过结合来自预测元素的这三个约束，本文生成Ax = 0形式的线性系统，其中A为矩阵，其维数为（3 | K | +3 | E | + | S |）×12 。 x = [rT 1 ， rT 2 ， rT 3 ， tT] T 12×1是一个向量，在单个空间中包含旋转和平移参数。为了建模关键点，边缘向量和对称对应之间的相对重要性，本文分别通过超参数αE和αS缩放（2）和（3），以生成A 。
根据EPnP ，本文将x计算为
文章插图
其中vi是A的第i个最小的右奇异矢量。理想情况下，当预测元素无噪声时， N = 1且x = v1是最佳解决方案。但是，这种策略在给出嘈杂预测的情况下效果不佳。与EPnP相同，本文选择N =4 。为计算最佳x ，本文通过以下目标函数的交替优化程序对潜变量γi和旋转矩阵R进行优化：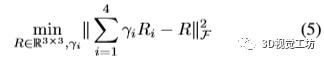
文章插图
其中， Ri∈R3×3是从vi的前9个元素重塑而成的。在获得最佳γi之后，本文将得到的精细变换P4 i = 1γiRi投影为刚性变换。由于篇幅所限，本文将细节推迟到补充材料上。
优化子模块。尽管（5）结合了混合中间表示形式并接受了良好的初始化，但它并不直接对预测元素中的异常值建模。另一个限制来自（1）和（2），它们不能最小化投影误差（即，关于关键点和边缘），而投影误差在基于界标的位姿估计中是有效的。
受益于具有初始对象位姿（Rinit ， tinit），优化子模块执行局部优化以优化对象位姿。本文介绍了两个涉及投影误差的差异向量：?k ， e ， s ，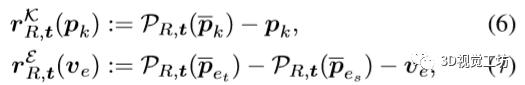
文章插图
其中PR ， t：R3→R2是从当前姿态（R ， t）导出的投影算符。
为了修剪预测元素中的异常值，本文考虑广义的German-Mcclure（或GM）鲁棒函数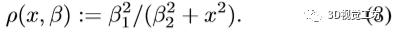
文章插图
通过此设置， HybridPose解决了以下用于姿态优化的非线性优化问题：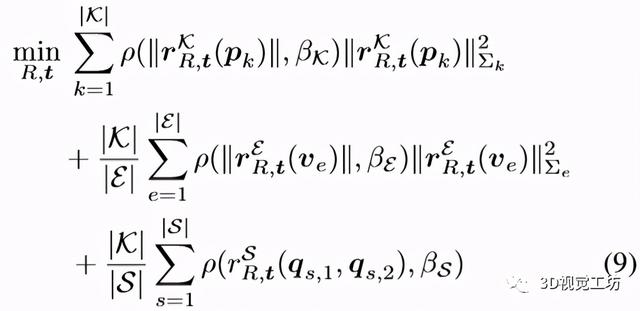
文章插图
其中βK ， βE和βS是关键点，边缘和对称对应关系的单独的超参数。 Σk和Σe表示附加到关键点和边缘预测的协方差信息。 kxkA =（xTAx）1 2.当预测的协方差不可用时，本文只需设置Σk=Σe= I2 。
从R init和t init开始，微调子模块采用Gauss-Newton方法进行数值优化。
2.4 HybridPose训练本节介绍如何使用标记的数据集T = {I ，（Kgt I ， Egt I ， Sgt I ，（Rgt I ， tgt I））}训练HybridPose的预测网络和超参数。使用I ， Kgt I ， Egt I ， Sgt I和（Rgt I ， tgt I），本文分别表示RGB图像，标记的关键点，边缘，对称对应关系和真值标定物体位姿。一种流行的策略是端到端训练整个模型，例如使用循环网络对优化过程进行建模，并在对象姿态输出以及中间表示上引入损耗项。但是，本文发现此策略不理想。训练集上预测元素的分布与测试集上的分布不同。即使通过仔细调整对预测元素的监督与最终对象位姿之间的权衡，适合训练数据的位姿回归模型也无法很好地概括测试数据。