HybridPose：混合表示下的6D对象姿态估计作者：康斯坦奇来源：公众号

作者：康斯坦奇
来源：公众号@计算机视觉工坊|系投稿
论文题目：HybridPose: 6D Object Pose Estimation under Hy Representations
论文地址：在公众号「3D视觉工坊」后台，回复「6D对象姿态估计」，即可直接下载。
摘要：本文介绍了HybridPose ，这是一种新颖的6D对象姿态估计方法。 HybridPose利用混合中间表示在输入图像中表达不同的几何信息，包括关键点，边缘矢量和对称对应关系。与单一表示相比，当一种类型的预测表示不准确时（例如，由于遮挡），本文的混合表示允许位姿回归利用更多不同的特征。 HybridPose利用强大的回归模块来过滤预测的中间表示中的异常值。本文通过证明可以通过相同的简单神经网络预测所有中间表示而无需牺牲整体性能来展示HybridPose的鲁棒性。与最新的位姿估计方法相比， HybridPose在运行时间上具有可比性，并且准确性更高。例如，在Occlusion Linemod数据集上，本文的方法实现了30 fps的预测速度，平均ADD（-S）精度为79.2％，比当前的最新方法提高了67.4％。
一、简介在本文中，本文介绍了HybridPose ，它利用多个中间表示来表达输入图像中的几何信息以进行位姿估计。除关键点外， HybridPose还集成了一个预测网络，该网络可以输出相邻关键点之间的边缘矢量，如图1所示。由于大多数对象都具有（部分）反射对称性，因此HybridPose还利用了预测的密集逐像素对应关系，这些对应关系反映了像素之间的基本对称关系。
文章插图
图1. HybridPose预测关键点，边缘向量和对称性对应。在（a）中，本文显示输入的RGB图像，其中感兴趣的对象（钻孔器）被部分遮挡。在（b）中，红色标记表示预测的2D关键点。在（c）中，边缘向量由所有关键点之间的有效连接图定义。在（d）中，对称对应关系将对象上的每个2D像素连接到其对称对应对象。为了说明的目的，在此示例中，本文仅从5755个预测对象像素中绘制了50个随机样本的对称对应关系。通过将预测与3D模板共同对齐来获得预测姿态（f），这涉及解决非线性优化问题。
二、方法HybridPose的输入是一个图像I ，其中包含一个已知类的对象，该图像由针孔照相机以已知的固有参数拍摄。假设对象类别具有标准坐标系Σ（即3D点云）， HybridPose在Σ下输出图像对象的6D相机姿态（RI∈SO（3）， tI∈R3），其中RI是旋转组件，而tI是平移组件。
2.1 方法概述如图2所示， HybridPose由预测模块和位姿回归模块组成。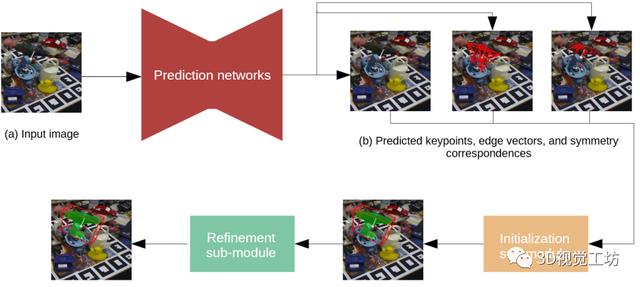
文章插图
图2.方法概述。 HybridPose由中间表示预测网络和位姿回归模块组成。预测网络将图像作为输入，并输出预测的关键点，边缘矢量和对称对应关系。姿态回归模块由初始化子模块和优化子模块组成。初始化子模块使用预测的中间表示法求解线性系统以获得初始姿态。改进子模块利用GM鲁棒范数进行优化（9），以获得最终的姿态预测。
2.2 混合表示本节描述了“混合位姿”中使用的三种中间表示形式。
关键点。第一个中间表示由关键点组成，这些关键点已被广泛用于位姿估计。给定输入图像I ，本文训练一个神经网络fKθ（I）∈R2×| K | 。预测| K |的预定义集合的2D关键点坐标。在本文的实验中， HybridPose使用了称为PVNet的现成模型，该模型是基于关键点的最新姿态估计器，可以采用投票方案来预测可见和不可见的关键点。
边缘。第二个中间表示由沿着预先定义的图的边缘向量组成，显式地模拟每对关键点之间的位移。如图2所示， HybridPose利用简单网络fEφ（I）∈R2×| E | 。预测2D图像平面中的边缘矢量，其中| E |表示预定图形中的边缘数。在本文的实验中， E是一个完全连通的图，即| E | = | K |·（|| K | ?1）/2 。
对称性对应。第三中间表示由反映基础反射对称性的预测像素方向对称性对应组成。在本文的实验中， HybridPose扩展了FlowNet 2.0的网络架构，该架构结合了密集的像素流和PVNet预测的语义掩码。通过在掩膜区域内预测像素方向的流量，可以得出所得的对称性对应关系。与前两种表示相比，对称对应的数量大得多，甚至为被遮挡的对象也提供了丰富的约束。但是，对称对应仅约束对象旋转分量的两个自由度。有必要将对称对应与其他中间表示相结合。
网络设计摘要。在本文的实验中， fKθ（I）， fEφ（I）和fSγ均基于ResNet ，具体实现细节在4.1节中讨论。可训练参数在除最后一个卷积层之外的所有参数之间共享。因此，引入边缘预测网络fEφ（I）和对称预测网络fSγ的开销微不足道。