AlphaGo原来是这样运行的，一文详解多智能体强化学习( 六 ) 机器之心分析师网络作者：杨

这样的分解方式，在联合动作 Q 值的结构组成方面考虑了个体行为的特性，使得该 Q 值更易于学习。另一方面，它也能够适配集中式的训练方式，在一定程度上能够克服多智能体系统中环境不稳定的问题。在训练过程中，通过联合动作 Q 值来指导策略的优化，同时个体从全局 Q 值中提取局部的 Qi 值来完成各自的决策（如贪心策略 ai=argmax Qi），实现多智能体系统的分布式控制。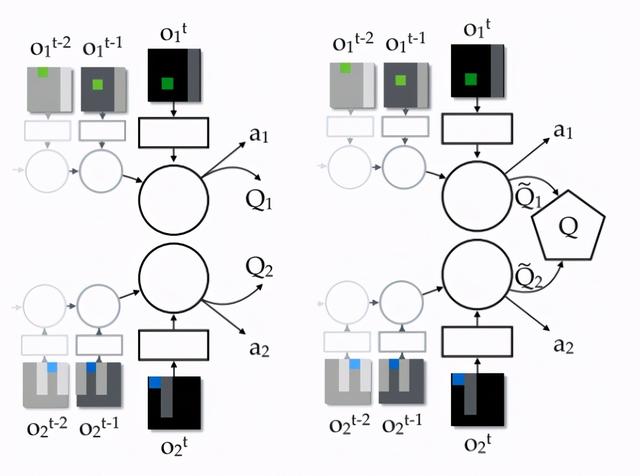
文章插图
图 9：左图是完全分布式的局部 Q 值网络结构，右图是 VDN 的联合动作 Q 值网络结构。考虑两个智能体，它们的联合动作 Q 值由个体的 Q1 和 Q2 求和得到，在学习时针对这个联合 Q 值进行迭代更新，而在执行时个体根据各自的 Qi 值得到自身的动作 ai 。图源：[11]
VDN 对于智能体之间的关系有较强的假设，但是，这样的假设并不一定适合所有合作式多智能体问题。在 2018 年的 ICML 会议上，有研究者提出了改进的方法 QMIX 。
文章插图
QMIX 在 VDN 的基础上实现了两点改进：1）在训练过程中加入全局信息进行辅助；2）采用混合网络对单智能体的局部值函数进行合并（而不是简单的线性相加）。
在 QMIX 方法中，首先假设了全局 Q 值和局部 Q 值之间满足这样的关系：最大化全局 Q_tot 值对应的动作，是最大化各个局部 Q_a 值对应动作的组合，即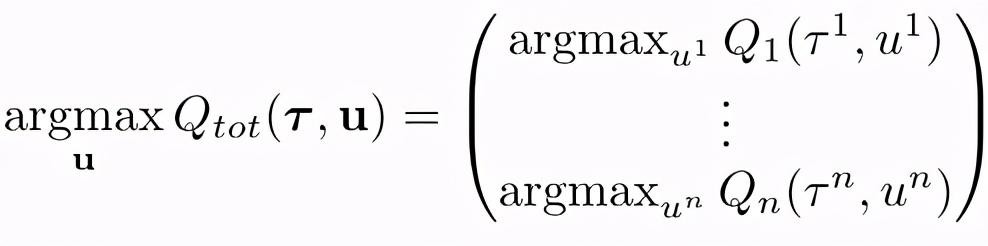
文章插图
在这样的约束条件下，既能够使用集中式的学习方法来处理环境不稳定性问题以及考虑多智能体的联合动作效应（全局 Q 值的学习），又能够从中提取出个体策略实现分布式的控制（基于局部 Q 值的行为选择）。进一步地，该约束条件可转化为全局 Q 值和局部 Q 值之间的单调性约束关系：
令全局 Q 值和局部 Q 值之间满足该约束关系的函数表达式有多种， VDN 方法的加权求和就是其中一种，但简单的线性求和并没有充分考虑到不同个体的特性，对全体行为和局部行为之间的关系的描述有一定的局限性。 QMIX 采用了一个混合网络模块（mixing network）作为整合 Qa 生成 Q_tot 的函数表达式，它能够满足上述的单调性约束。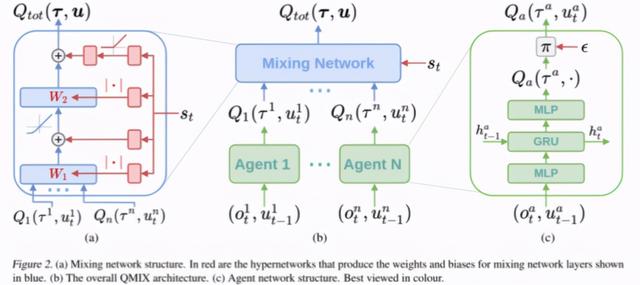
文章插图
图 10：QMIX 网络结构。图源：[12]
在 QMIX 方法设计的网络结构中，每个智能体都拥有一个 DRQN 网络（绿色块），该网络以个体的观测值作为输入，使用循环神经网络来保留和利用历史信息，输出个体的局部 Qi 值。
所有个体的局部 Qi 值输入混合网络模块（蓝色块），在该模块中，各层的权值是利用一个超网络（hypernetwork）以及绝对值计算产生的：绝对值计算保证了权值是非负的、使得局部 Q 值的整合满足单调性约束；利用全局状态 s 经过超网络来产生权值，能够更加充分和灵活地利用全局信息来估计联合动作的 Q 值，在一定程度上有助于全局 Q 值的学习和收敛。
结合 DQN 的思想，以 Q_tot 作为迭代更新的目标，在每次迭代中根据 Q_tot 来选择各个智能体的动作，有：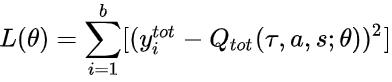
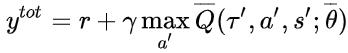文章插图
文章插图
最终学习收敛到最优的 Q_tot 并推出对应的策略，即为 QMIX 方法的整个学习流程。
3. 多智能体强化学习的应用
3.1. 游戏应用
分步对抗游戏
这类游戏包括了围棋、国际象棋、扑克牌等， MARL 在这几种游戏中都有相关的研究进展并取得了不错的成果。其中，著名的 AlphaGo 通过在和人类对战的围棋比赛中取得的惊人成绩而进入人们的视野。围棋是一种双玩家零和随机博弈，在每个时刻，玩家都能够获取整个棋局。它一种涉及超大状态空间的回合制游戏，很难直接使用传统的 RL 方法或者是搜索方法。 AlphaGo 结合了深度学习和强化学习的方法：
针对巨大状态空间的问题，使用网络结构 CNN 来提取和表示状态信息；
在训练的第一个阶段，使用人类玩家的数据进行有监督训练，得到预训练的网络；
在训练的第二个阶段，通过强化学习方法和自我博弈进一步更新网络；
在实际参与游戏时，结合价值网络（value network）和策略网络（policy network），使用蒙特卡洛树搜索（MCTS）方法得到真正执行的动作。