AlphaGo原来是这样运行的,一文详解多智能体强化学习
机器之心分析师网络
作者:杨旭韵
编辑:Joni
在这篇综述性文章中 , 作者详尽地介绍了多智能强化学习的理论基础 , 并阐述了解决各类多智能问题的经典算法 。 此外 , 作者还以 AlphaGo、AlphaStar为例 , 概述了多智能体强化学习的实际应用 。
近年来 , 随着强化学习(reinforcement learning)在多个应用领域取得了令人瞩目的成果 , 并且考虑到在现实场景中通常会同时存在多个决策个体(智能体) , 部分研究者逐渐将眼光从单智能体领域延伸到多智能体 。
本文将首先简要地介绍多智能体强化学习(multi-agent reinforcement learning, MARL)的相关理论基础 , 包括问题的定义、问题的建模 , 以及涉及到的核心思想和概念等 。 然后 , 根据具体应用中智能体之间的关系 , 将多智能体问题分为完全合作式、完全竞争式、混合关系式三种类型 , 并简要阐述解决各类多智能体问题的经典算法 。 最后 , 本文列举深度强化学习在多智能体研究工作中提出的一些方法(multi-agent deep reinforcement learning) 。
1. 强化学习和多智能体强化学习
我们知道 , 强化学习的核心思想是“试错”(trial-and-error):智能体通过与环境的交互 , 根据获得的反馈信息迭代地优化 。 在 RL 领域 , 待解决的问题通常被描述为马尔科夫决策过程 。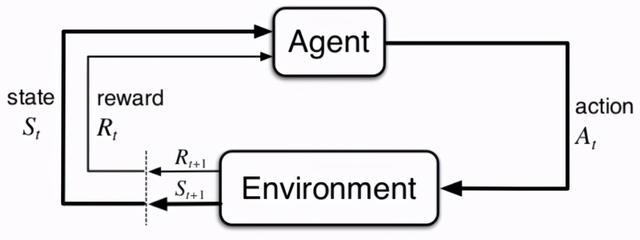 文章插图
文章插图
图 1:强化学习的框架(同时也表示了马尔科夫决策过程) 。 图源:[1]
当同时存在多个智能体与环境交互时 , 整个系统就变成一个多智能体系统(multi-agent system) 。 每个智能体仍然是遵循着强化学习的目标 , 也就是是最大化能够获得的累积回报 , 而此时环境全局状态的改变就和所有智能体的联合动作(joint action)相关了 。 因此在智能体策略学习的过程中 , 需要考虑联合动作的影响 。
1.1 多智能体问题的建模——博弈论基础
马尔科夫决策过程拓展到多智能体系统 , 被定义为马尔科夫博弈(又称为随机博弈 , Markov/stochastic game) 。 当我们对博弈论有一定了解后 , 能够借助博弈论来对多智能体强化学习问题进行建模 , 并更清晰地找到求解问题的方法 。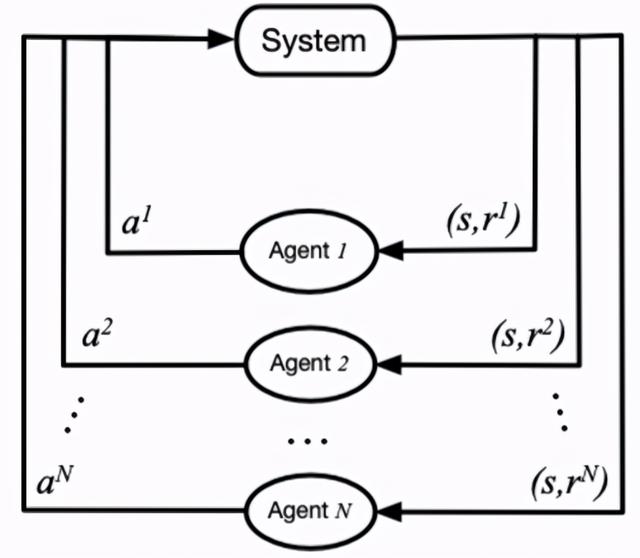 文章插图
文章插图
图 2:马尔科夫博弈过程 。 图源:[2]
在马尔科夫博弈中 , 所有智能体根据当前的环境状态(或者是观测值)来同时选择并执行各自的动作 , 该各自动作带来的联合动作影响了环境状态的转移和更新 , 并决定了智能体获得的奖励反馈 。 它可以通过元组 < S,A1,...,An,T,R1,...,Rn > 来表示 , 其中 S 表示状态集合 , Ai 和 Ri 分别表示智能体 i 的动作集合和奖励集合 , T 表示环境状态转移概率 , 表示损失因子 。 此时 , 某个智能体 i 获得的累积奖励的期望可以表示为: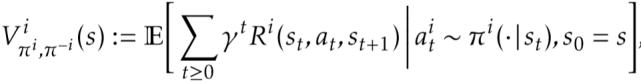 文章插图
文章插图
对于马尔科夫博弈 , 纳什均衡(Nash equilibrium)是一个很重要的概念 , 它是在多个智能体中达成的一个不动点 , 对于其中任意一个智能体来说 , 无法通过采取其他的策略来获得更高的累积回报 , 在数学形式上可以表达为: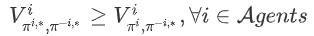 文章插图
文章插图
在该式中 , π^表示智能体 i 的纳什均衡策略 。
值得注意的是 , 纳什均衡不一定是全局最优 , 但它是在概率上最容易产生的结果 , 是在学习时较容易收敛到的状态 , 特别是如果当前智能体无法知道其他智能体将会采取怎样的策略 。 这里举个简单的例子来帮助理解 , 即博弈论中经典的囚徒困境 。 根据两个人不同的交代情况 , 判刑的时间是不一样的: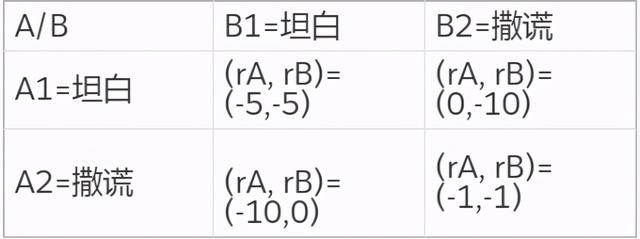 文章插图
文章插图
在这个表格中 , 当 A 和 B 都选择撒谎时 , 能够达到全局最优的回报 。 但是每个个体都不知道另外的个体会做出怎样的行为 , 对于 A 或者是来 B 说 , 如果改成选择坦白 , 则能够获得更优的回报 。 实际上 , 对于 A 或者 B 来说 , 此时不管另外的个体选择了哪种行为 , 坦白是它能够获得最优回报的选择 。 所以 , 最终会收敛到 A 和 B 都选择坦白 , 即囚徒困境中的纳什均衡策略 。
均衡求解方法是多智能体强化学习的基本方法 , 它对于多智能体学习的问题 , 结合了强化学习的经典方法(如 Q-learning)和博弈论中的均衡概念 , 通过 RL 的方法来求解该均衡目标 , 从而完成多智能体的相关任务 。 这种思路在后面介绍具体的学习方法中会有所体现 。
- 对手|一加9Pro全面曝光,或是小米11最大对手
- 行业|现在行业内客服托管费用是怎么算的
- 王兴称美团优选目前重点是建设核心能力;苏宁旗下云网万店融资60亿元;阿里小米拟增资居然之家|8点1氪 | 美团
- 手机基带|为了5G降低4G网速?中国移动回应来了:罪魁祸首不是运营商
- 技术|做“视频”绿厂是专业的,这项技术获人民日报评论点赞
- 互联网|苏宁跳出“零售商”重组互联网平台业务 融资60亿只是第一步
- 体验|闭上眼睛点外卖是什么感觉?时隔一年再次体验,进步令人欣慰
- 再次|华为Mate40Pro干瞪眼?P50再次曝光,这次是真香!
- 当初|这是我的第一部华为手机,当初花6799元买的,现在“一文不值”?
- 无国界|嘴上说着支持华为,却为苹果贡献了2000亿!还真是科技无国界啊?
