机器学习需要哪些数学基础？( 四 ) 机器学习是近几年炙手可热的

下面的代码中，通过逐步减小Δx来逼近差分值。代码如下。
initial_delta = .1x1 = 1for power in range (1,6):delta = pow (initial_delta, power)derivative_aprox= (quadratic(x1+delta) - quadratic (x1) )/((x1+delta) - x1 )print "delta: " + str(delta) + ", estimated derivative: " +str(derivative_aprox)在上面的代码中，首先定义了初始增量Δ ，从而获得初始近似值。然后在差分函数中，对0.1进行乘方运算，幂逐步增大， Δ的值逐步减小，得到如下结果。
delta: 0.1, estimated derivative: 4.2delta: 0.01, estimated derivative: 4.02delta: 0.001, estimated derivative: 4.002delta: 0.0001, estimated derivative: 4.0002delta: 1e-05, estimated derivative: 4.00002随着Δ值的逐步减小，变化率将稳定在4左右。但这个过程什么时候停止呢？事实上，这个过程可以是无限的，至少在数值意义上是这样。
这就引出了极限的概念。在定义极限的过程中，使 Δ 无限小，得到的结果称之为f(x)的导数或f ' (x) ，公式如下。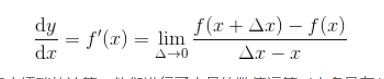
文章插图
但是数学家们并没有停止烦琐的计算。他们进行了大量的数值运算（大多是在17世纪手工完成的），并希望进一步简化这些操作。
现在构造一个函数，它可以通过替换x的值来得到相应的导数。对于不同的函数族，从抛物线(y=x2+b)开始，出现了更复杂的函数（见图1.17），这一巨大的进步发生在17世纪。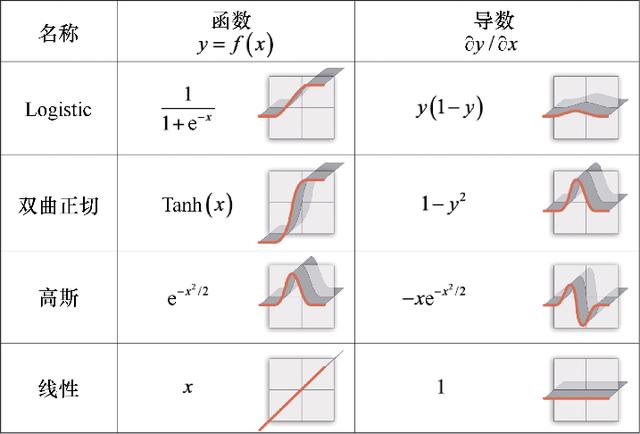
文章插图
图1.17　复杂函数
2．链式法则在函数导数符号确定后，一个非常重要的结果就是链式法则。莱布尼茨在1676年的一篇论文中首次提到这个公式。它可以通过非常简单优雅的方式求解复合函数的导数，从而简化复杂函数的求解。
为了定义链式法则，假设有一个函数f ， F=f (g(x)) ，那么导数可以定义如下。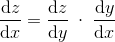
文章插图
链式法则允许对输入值为另一个函数的方程求导。这与搜索函数之间关联的变化率是一样的。链式法则是神经网络训练阶段的主要理论概念之一。因为在这些分层结构中，第一层神经元的输出将是下一层的输入。在大多数情况下，复合函数包含了一层以上的嵌套。
偏导数（Partial Derivative）到目前为止，本书一直使用单变量函数。但是从现在开始，将主要介绍多变量函数。因为数据集将不止包含一个列，并且它们中的每一列将代表不同的变量。
在许多情况下，需要知道函数在一个维度中的变化情况，这将涉及数据集的一列如何对函数的变化产生影响。
偏导数的计算包括将已知的推导规则应用到多变量函数，并把未被求导的变量作为常数导出。
看一看下面的幂函数求导法则。
f(x, y) = 2x3y
当这个函数对x求导时， y作为常量。可以将它重写为3 ? 2 y x2 ，并将导数应用到变量x ，得到以下结果。
d/dx(f(x, y)) = 6y * x2
使用这些方法，可以处理更复杂的多变量函数。这些函数将是特征集的一部分，通常由两个以上的变量组成。
本文摘自：《机器学习开发者指南》
文章插图
本书的目标读者是那些期望掌握机器学习的相关内容、理解主要的基本概念、使用算法思想并能掌握正式数学定义的开发人员。本书使用Python实现了代码概念， Python语言接口的简洁性，以及其提供的方便且丰富的工具，将有助于我们处理这些代码，而有其他编程语言经验的程序员也能理解书中的代码。
读者将学会使用不同类型的算法来解决自己的机器学习相关问题，并了解如何使用这些算法优化模型以得到最佳的结果。如果想要了解现在的机器学习知识和一门友好的编程语言，并且真正走进机器学习的世界，那么这本书一定能对读者有所帮助。
【机器学习需要哪些数学基础？】本书主要关注机器学习的相关概念，并使用Python语言（版本3）作为编码工具。本书通过Python 3和Jupyter Notebook来构建工作环境，可以通过编辑和运行它们来更好地理解这些概念。我们专注于如何以最佳方式，利用各种Python库来构建实际的应用程序。本着这种精神，我们尽力使所有代码保持友好性和可读性，使读者能够轻松地理解代码并在不同的场景中使用它们。