机器学习需要哪些数学基础？( 三 ) 机器学习是近几年炙手可热的

结果如图1.12所示。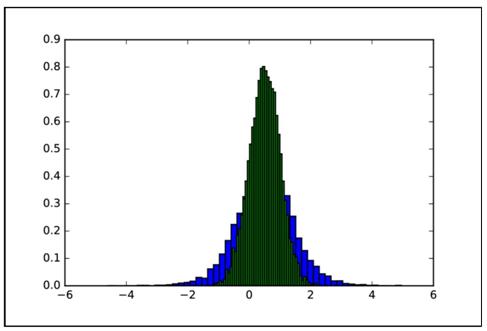
文章插图
图1.12　Logistic分布（绿）和正态分布（蓝）[1]
如前所述，计算Logistic分布的积累分布函数时，读者将看到一个非常熟悉的图形，即Sigmoid曲线。后面在回顾神经网络激活函数时，还将再次看到它。代码如下。
plt.figure()logistic_cumulative = np.random.logistic(mu, sigma, 10000)/0.02plt.hist(logistic_cumulative, 50, normed=1, cumulative=True)plt.show()结果如图1.13所示。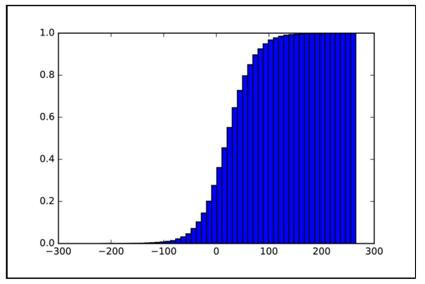
文章插图
图1.13　逆Logistic分布
1.3.3　概率函数的统计度量这一节中，将看到概率中常见的统计度量。首先是均值和方差，其定义与前面在统计学中看到的定义没有区别。
1．偏度（Skewness）它表示了一个概率分布的横向偏差，即偏离中心的程度或对称性（非对称性）。一般来说，如果偏度为负，则表示向右偏离；如果为正，则表示向左偏离。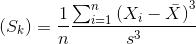
文章插图
图1.14描绘了偏度的统计分布。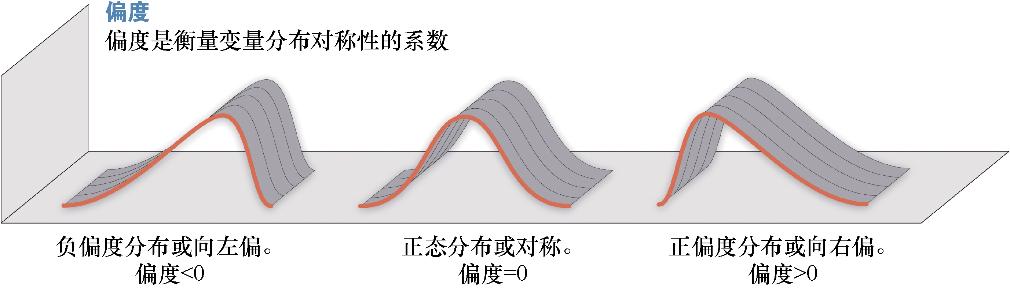
文章插图
图1.14　分布形状对偏度的影响
2．峰度（Kurtosis）峰度显示了分布的中心聚集程度。它定义了中心区域的锐度，也可以反过来理解，就是函数尾部的分布方式。
峰度的表达式如下。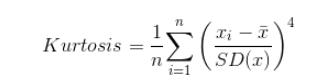
文章插图
由图1.15可以直观地理解这些新的度量。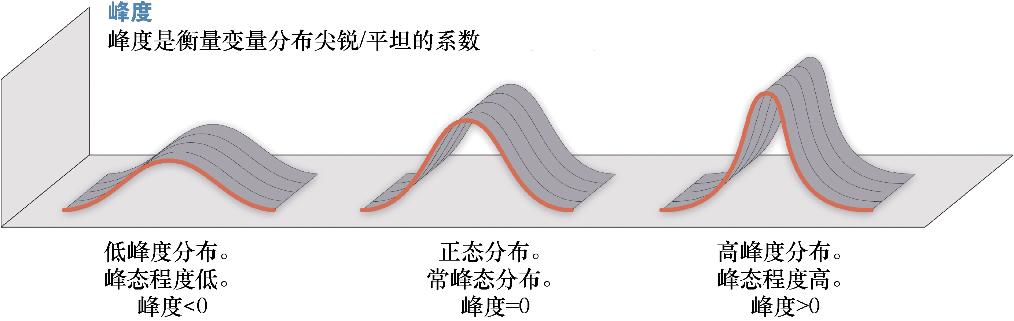
文章插图
图1.15　分布形状对峰度的影响
1.3.4　微分基础为了覆盖机器学习的基础知识，尤其是像梯度下降（Gradient Descent）这样的学习算法，本书将介绍微分学所涉及的概念。
1.3.5　预备知识介绍覆盖梯度下降理论所必需的微积分术语需要很多章节，因此我们假设读者已经理解连续函数的概念，如线性、二次、对数和指数，以及极限的概念。
为了清楚起见，我们将从一元函数的概念开始，然后简单地涉及多元函数。
1．变化分析——导数在前一节中介绍了函数的概念。除了在整个域中定义的常值函数之外，所有函数的值都是动态的。这意味着在x确定的情况下， f(x1)与f(x2)的值是不同的。
微分学的目的是衡量变化。对于这个特定的任务， 17世纪的许多数学家（莱布尼兹和牛顿是杰出的倡导者）努力寻找一个简单的模型来衡量和预测符号定义的函数如何随时间变化。
这项研究将引出一个奇妙的概念—— 一个具有象征性的结果，在一定条件下，表示在某个点上函数变化的程度，以及变化的方向。这就是导数的概念。
在斜线上滑动如果想测量函数随时间的变化，首先要取一个函数值，在其后的点上测量函数。第一个值减去第二个值，就得到函数随时间变化的程度。代码如下。
import matplotlib.pyplot as pltimport numpy as np %matplotlib inlinedef quadratic(var):return 2* pow(var,2)x=np.arange(0,.5,.1)plt.plot(x,quadratic(x))plt.plot([1,4], [quadratic(1), quadratic(4)], linewidth=2.0)plt.plot([1,4], [quadratic(1), quadratic(1)], linewidth=3.0,label="Change in x")plt.plot([4,4], [quadratic(1), quadratic(4)], linewidth=3.0,label="Change in y")plt.legend()plt.plot (x, 10*x -8 )plt.plot()前面的代码示例首先定义了一个二次方程（2×x2），然后定义arange函数的域（0～0.5 ，步长0.1）。
定义一个区间，测量y随x的变化，并画出测量的直线，如图1.16所示。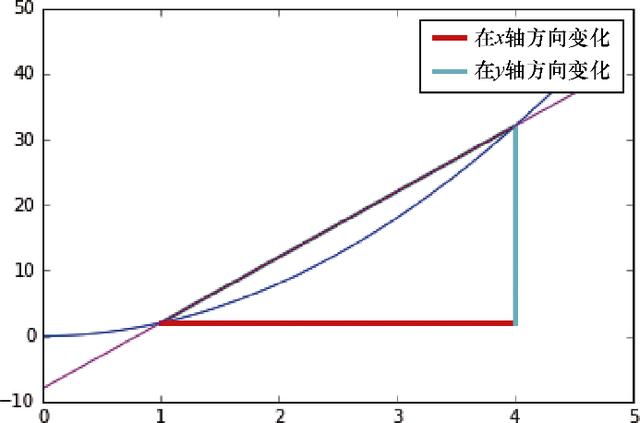
文章插图
图1.16　求导操作起始设置的初始描述
在x=1和x=4处测量函数，并定义这个区间的变化率。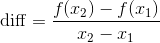
文章插图
根据公式，示例程序的运行结果是(36?0)/3=12 。
这个方法可以用来近似测量，但它太依赖于测量的点，并且必须在每个时间间隔都进行测量。
为了更好地理解函数的动态变化，需要能够定义和测量函数域中每个点的瞬时变化率。因为是测量瞬时变化，所以需要减少域x值之间的距离，使各点之间的距离尽量缩短。我们使用初始值x和后续值x + Δx来表示这个方法。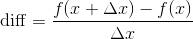
文章插图