机器学习需要哪些数学基础？机器学习是近几年炙手可热的

机器学习是近几年炙手可热的话题。每天都有新的应用和模型进入人们的视野。世界各地的研究人员每天所公布的实验结果都显示了机器学习领域所取得的巨大进步。
技术工作者参加各类课程、搜集各种资料，希望使用这些新技术改进他们的应用。但在很多情形下，要理解机器学习需要深厚的数学功底。这就为那些虽然具有良好的算法技能，但数学概念欠佳的程序员们设置了较高的门槛。
为了掌握它们背后的动机和理论，有必要回顾并建立所有基本推理知识体系，包括统计、概率和微积分。
下面先从一些基本的统计概念开始。
1.3.1　统计学——不确定性建模的基本支柱统计学可以定义为使用数据样本，提取和支持关于更大样本数据结论的学科。考虑到机器学习是研究数据属性和数据赋值的重要组成部分，本书将使用许多统计概念来定义和证明不同的方法。
描述性统计学——主要操作接下来将从定义统计学的基本操作和措施入手，并将基本概念作为起点。
（1）平均值（Mean）
这是统计学中直观、常用的概念。给定一组数字，该集合的平均值是所有元素之和除以集合中元素的数量。
平均值的公式如下。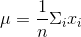
文章插图
虽然这是一个非常简单的概念，但本书还是提供了一个Python代码示例。在这个示例中，我们将创建样本集，并用线图表示它，将整个集合的平均值标记为线，这条线应该位于样本的加权中心。它既可以作为Python语法的介绍，也可以当作Jupyter Notebook的实验。代码如下。
import matplotlib.pyplot as plt #Import the plot librarydef mean(sampleset):#Definition header for the mean functiontotal=0for element in sampleset:total=total+elementreturn total/len(sampleset)myset=[2.,10.,3.,6.,4.,6.,10.] #We create the data setmymean=mean(myset) #Call the mean funcionplt.plot(myset)#Plot the datasetplt.plot([mymean] * 7)#Plot a line of 7 points located on the mean该程序将输出数据集元素的时间序列，然后在平均高度上绘制一条线。
如图1.6所示，平均值是描述样本集趋势的一种简洁（单值）的方式。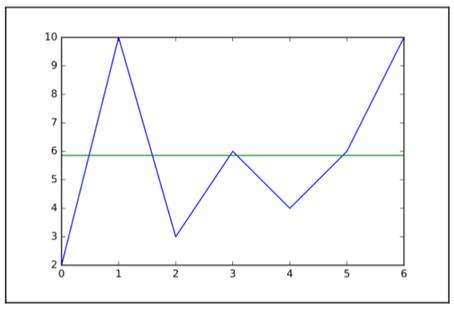
文章插图
图1.6　用平均值描述样本集趋势
因为在第一个例子中，我们使用了一个非常均匀的样本集，所以均值能够有效地反映这些样本值。
下面再尝试用一个非常分散的样本集（鼓励读者使用这些值）来进行实验，如图1.7所示。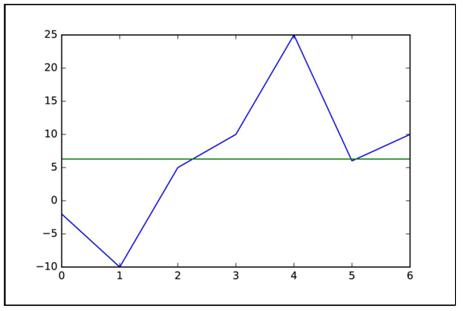
文章插图
图1.7　分散样本集的趋势
（2）方差（Variance）
正如前面的例子所示，平均值不足以描述非均匀或非常分散的样本数据。
为了使用一个唯一的值来描述样本值的分散程度，需要介绍方差的概念。它需要将样本集的平均值作为起点，然后对样本值到平均值的距离取平均值。方差越大，样本集越分散。
方差的规范定义如下。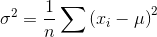
文章插图
下面采用以前使用的库，编写示例代码来说明这个概念。为了清楚起见，这里重复mean函数的声明。代码如下。
import math #This library is needed for the power operationdef mean(sampleset):#Definition header for the mean functiontotal=0for element in sampleset:total=total+elementreturn total/len(sampleset)def variance(sampleset):#Definition header for the mean functiontotal=0setmean=mean(sampleset)for element in sampleset:total=total+(math.pow(element-setmean,2))return total/len(sampleset)myset1=[2.,10.,3.,6.,4.,6.,10.]#We create the data setmyset2=[1.,-100.,15.,-100.,21.]print "Variance of first set:" + str(variance(myset1))print "Variance of second set:" + str(variance(myset2))前面的代码将输出以下结果。
Variance of first set:8.69387755102Variance of second set:3070.64正如上面的结果所示，当样本值非常分散时，第二组的方差要高得多。因为计算距离平方的均值是一个二次运算，它有助于表示出它们之间的差异。
（3）标准差（Standard Deviation）
标准差只是对方差中使用的均方值的平方性质进行正则化的一种手段。它有效地将该项线性化。这个方法可以用于其他更复杂的操作。
以下是标准差的表示形式。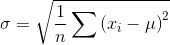
文章插图
1.3.2　概率与随机变量概率与随机变量对于理解本书所涉概念极为重要。