概率（Probability）是一门数学学科 ， 它的主要目标就是研究随机事件 。 从实际的角度讲 ， 概率试图从可能发生的所有事件中量化事件发生的确定性（或者不确定性） 。
1．事件为了理解概率 ， 我们首先对事件进行定义 。 在给定的实验中 ， 执行确定的动作可能出现不同的结果 。 事件就是该实验中所有可能结果的子集 。
关于事件的一个例子就是摇骰子时出现的特定数字 ， 或者装配线上出现的某种产品缺陷 。
（1）概率
按照前面的定义 ， 概率是事件发生的可能性 。 概率被量化为0～1之间的实数 。 当事件发生的可能性增加时 ， 概率P也按照接近于1的趋势增加 。 事件发生概率的数学表达式是P(E) 。
（2）随机变量和分布
在分配事件概率时 ， 可以尝试覆盖整个样本 ， 并为样本空间中的每个可能分配一个概率值 。
这个过程具有函数的所有特征 。 对于每一个随机变量 ， 都会为其可能的事件结果进行赋值 。 这个函数称为随机函数 。
这些变量有以下两种类型 。

• 离散（Discrete）：结果的数量是有限的或可数无穷的 。
• 连续（Continuous）：结果集属于连续区间 。

这个概率函数也称为概率分布（Probability Distribution） 。
2．常用概率分布在多种可能的概率分布中 ， 有些函数由于其特殊的性质或它们所代表问题的普遍性而被研究和分析 。
本书将描述那些常见的概率分布 。 它们对机器学习的发展具有特殊的影响 。
（1）伯努利分布（Bernoulli Distribution）
从一个简单的分布开始：像抛硬币一样 ， 它具有二分类结果（binary outcome） 。
这个分布表示单个事件 。 该事件中1（正面）的概率为p ， 0（反面）的概率为1?p 。
为了实现可视化 ， 可以使用np（NumPy库）生成大量伯努利分布的事件 ， 并绘制该分布的趋势 。 它有以下两种可能的结果 。 代码如下 。
plt.figure()distro = np.random.binomial(1, .6, 10000)/0.5plt.hist(distro, 2 , normed=1)下面通过图1.8中的直方图显示二项分布（Binomial Distribution） ， 可以看出结果概率的互补性质 。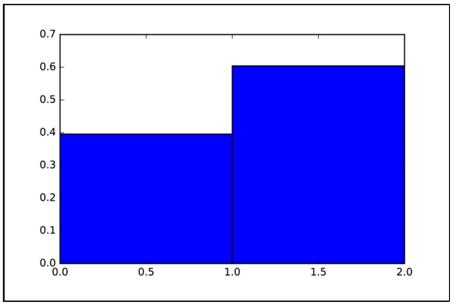
文章插图
图1.8　二项分布
可能结果的概率互补趋势非常明显 。 现在用更多的可能结果来补充模型 。 当结果的数目大于2时 ， 采用多项式分布（Multinomial Distribution） 。 代码如下 。
plt.figure()distro = np.random.binomial(100, .6, 10000)/0.01plt.hist(distro, 100 , normed=1)plt.show()结果如图1.9所示 。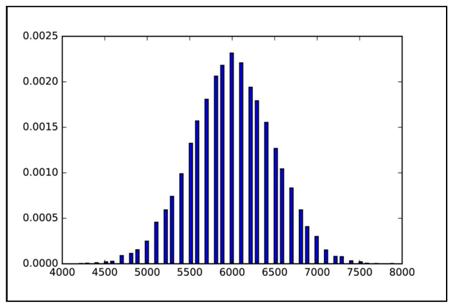
文章插图
图1.9　100种可能结果的多项式分布
（2）均匀分布（Uniform Distribution）
这种非常常见的分布是本书出现的第一个连续分布 。 顾名思义 ， 对于域的任何区间 ， 它都有一个恒定的概率值 。
a和b是函数的极值 ， 为了使函数积分为1 ， 这个概率值为1/(b?a) 。
下面用一个非常规则的直方图生成样本均匀分布的图 。 代码如下 。
plt.figure()uniform_low=0.25uniform_high=0.8plt.hist(uniform, 50, normed=1)plt.show()结果如图1.10所示 。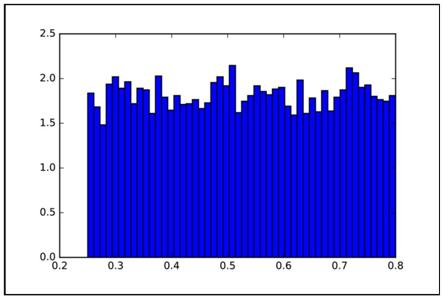
文章插图
图1.10　均匀分布
（3）正态分布（Normal Distribution）
这是一种常见的连续随机函数 ， 也称作高斯函数（Gaussian Function） 。 虽然表达式有些复杂 ， 但它只需要用均值和方差来定义 。
这是函数的标准形式 。
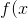文章插图
查看下面的代码 。
import matplotlib.pyplot as plt #Import the plot libraryimport numpy as npmu=0.sigma=2.distro = np.random.normal(mu, sigma, 10000)plt.hist(distro, 100, normed=True)plt.show()图1.11所示为生成的分布直方图 。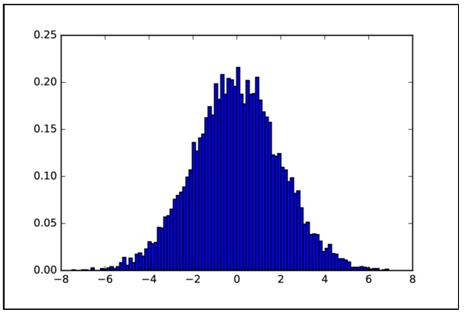
文章插图
图1.11　正态分布
（4）Logistic分布（Logistic Distribution）
它类似于正态分布 ， 但在形态上与正态分布存在较大差异 ， 其具有细长的尾部 。 它的重要性在于积累分布函数（Cumulative Distribution Function ， CDF） ， 下面的章节中将会使用到它 ， 读者会觉得它看起来很熟悉 。
下面这段代码表示了它的基本分布 。
import matplotlib.pyplot as plt #Import the plot libraryimport numpy as npmu=0.5sigma=0.5distro2 = np.random.logistic(mu, sigma, 10000)plt.hist(distro2, 50, normed=True)distro = np.random.normal(mu, sigma, 10000)plt.hist(distro, 50, normed=True)plt.show()

• 上一页
• 1
• 2
• 3
• 4
• 下一页

• 机器人|网络里面的假消息忽悠了非常多的小喷子和小机器人
• 跑腿|机器人“小北”上岗 让办事群众少跑腿
• 计算机学科|机器视觉系统是什么
• 机器人|外骨骼康复训练机器人助力下肢运动功能障碍患者康复训练
• 人类|距离人类“玩坏”自己的电脑桌面，还需要多久？
• 加急|古代8百里加急究竟有多快？需要骑马20个小时，速度媲美顺丰快递！
• 教学|机器人教学的目标方案
• 体验|VR\/AR体验、3D打印、机器人“对决”……松江这所中学人工智能创新实验室真的赞
• 输送|新时达：“用于机器人码垛的输送系统”获发明专利
• 操作|[LIVE On]黄敏贤和郑多彬充满心碎的下午：机器操作每次都不能通过测试