联合分布|「AI课堂」深度学习中的熵（理论篇）机器学习你会遇到的“坑”( 二 ) 回顾信息熵我们在《非参数模

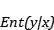文章插图
。如果随机变量x的分布与联合分布一致，说明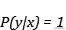
文章插图
，条件熵为零。条件熵衡量的正是随机变量x与联合分布的差异！
我们可以继续将对数内的除法化作对数外的减法，可以得到：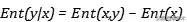
文章插图
我们可以将其理解为，存在两个随机变量的系统熵就是联合熵，当我们确定了其中一个变量，不确定程度就减弱了，那么这个变量所携带的熵就可以被减去，得到的正是条件熵。正好与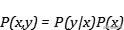
文章插图
相对应。
文章插图
相对熵和交叉熵
如果我们可以通过信息熵顺利的理解互信息和条件熵，那么相对熵和交叉熵将变得非常简单。
互信息的办法为我们提供了一条非常重要的思路，我们可以通过概率分布的信息熵比较两个分布的依赖性质，那么是不是也可以通过信息熵比较两个分布的差异呢？
有人会认为，我们将两个分布的信息熵做差就可以间接衡量分布的差异，但是这样做得到只是两个分布不确定程度的比较，而非分布本身的差异。我们在上文曾经说，条件熵衡量的正是随机变量与联合分布的差异，那么推广到其他分布，我们只需要在改变自信息就可以达到衡量分布差异的目的！
所谓的相对熵（relative entropy ），又称KL散度，就是将自信息变为两个分布的差来衡量分布的差异,假设两个分布P、Q：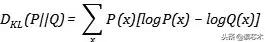
文章插图
就得到了分布差作为自信息在某一分布下的期望值。从公式中可以看出相对熵并不对称的，即：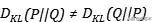
文章插图
我们可以不用编码长度这类知识去理解这样的不对称性，只需要利用一个我们已经知道的事实，即一般情况下，条件熵本身就是不对称的，我们把Q看作联合分布或者把P看作联合分布，所得出的就是两个条件熵。
如果我们在相对熵的基础上加上某一分布所具有的信息熵，就会得到交叉熵（cross entropy）: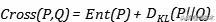
文章插图
交叉熵经常被用作损失函数，我们在上一节曾经给出了sigmoid函数作为伯努利分布的logistic回归的极大似然估计，那么我们如果使用交叉熵作为损失函数，假设的概率由sigmoid函数给出，实际的概率由数据出给：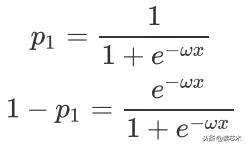
文章插图
【联合分布|「AI课堂」深度学习中的熵（理论篇）机器学习你会遇到的“坑”】对其做最小化可以自然的得到极大似然估计的形式，因为我们根据交叉熵的定义可以直接写出：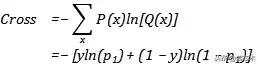
文章插图
文章插图
最大熵原则
在物理的热力学中，等概率原理下的经典粒子的玻尔兹曼分布，其实也对应着最大熵原理，因为等概率对应就是均匀分布。在很多情况下，对事件假设高熵分布，保留尽可能多的不确定性，是最为安全的做法，就好像一枚骰子，如果对其信息一无所知，很自然就可以假设其六个面的概率均为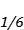
文章插图
。还比如，我们经常使用的高斯分布，就是在标准差和均值已知前提下，熵最大的分布。
我们曾经利用指数分布和广义线性模型推导出了softmax函数，但同时我们还可以根据最大熵模型给出softmax函数。
很多教材上都会详细讲解在约束优化下的最大熵原则导出的推断，此处因为篇幅关系，我不做详细讲解，只利用一个很重要的结论，我们用i来标记样本，用j来标记可能的结果，那么最大熵模型会给出：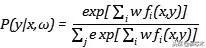
文章插图
其中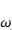
文章插图
是参数，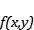
文章插图