联合分布|「AI课堂」深度学习中的熵(理论篇)机器学习你会遇到的“坑”
 文章插图
文章插图 文章插图
文章插图
回顾信息熵
我们在《非参数模型》介绍决策树时 , 引入了自信息和信息熵的概念 。
? 自信息(self-information):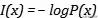 文章插图
文章插图
, 是从概率角度出发对信息量的刻画 。 对概率取对数 , 是为了满足联合概率的信息的可加性 , 即两个事件均发生的概率要相乘 , 但反映在信息量上要相加;再取负值 , 是因为小概率的事件信息量更大 , 大概率事件的信息量更小 。
? 信息熵(Information Entropy): 文章插图
文章插图
, 是自信息的期望值 , 即来自于一个概率分布的自信息的加权平均 。
我们得到的熵是一个关于自变量的函数 , 当自变量均匀分布时会取到最大值 , 当均匀分布 , 自变量的在可能状态概率是相等的 , 所以我们也罢均匀分布叫做等概率分布 。 均匀分布下 , 我们可以进一步的增加变量的可能状态数来增加变量的不确定性 , 而变量的不确定性越大 , 相应的信息熵就会越大 。 这正是我们在决策树中利用信息增益率来改进信息熵的原因 。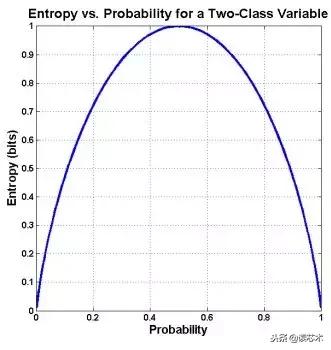 文章插图
文章插图
如图 , 考虑只有两种结果的随机变量 , 横轴为其中一个结果的概率 , 当概率为0.5时 , 信息熵达到最大,还可以看到当变量不存在任何的不确定性时 , 比如在左右两端时 , 信息熵为零 。
在此基础上 , 我们非常容易地可以将熵的概念扩展 , 有概率分布的地方 , 就可以定义相应的熵 。
比如 , 两个随机变量存在联合概率 , 我们很容易引入联合熵: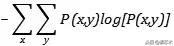 文章插图
文章插图
如果两个变量相互独立 , 因为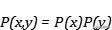 文章插图
文章插图
就有: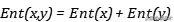 文章插图
文章插图
即两个独立变量携带熵之和就是其联合分布的熵 。 我们还会在很多地方看到所谓的互信息(Mutual Information ) , 在信息熵的基础上就变得非常好理解 , 将两个随机变量的熵分别加起来然后减去其联合熵: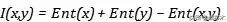 文章插图
文章插图
如果其不为零 , 说明两个随机变量并不相互独立 , 值越大 , 说明关联程度越高 。
如果两个随机变量存在依赖关系 , 可能会出现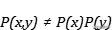 文章插图
文章插图
, 那么条件概率就有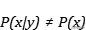 文章插图
文章插图
, 就有条件熵: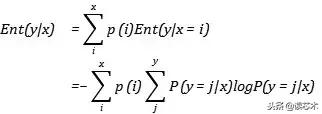 文章插图
文章插图
我们可以将条件熵理解为随机变量在另一特定的随机变量下的条件熵取遍所有可能性的结果 , 而第一个式子右边的需要求和的熵正是针对特定的x定义的条件熵 , 最后我们将所有x下的条件熵进行加权平均 , 得到最后的条件熵 。 本质上我们可以理解为条件熵描述了 , 在知道了随机变量x的前提下 , 随机变量y的信息熵的多少 。 这也说明 , 条件熵本身就是不对称的 。
我们可以将其展开得到: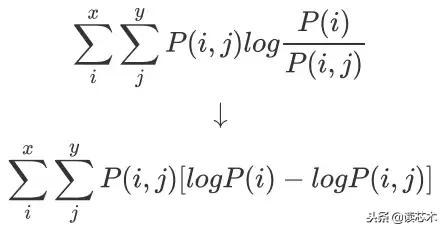 文章插图
文章插图
我们来分析两种极端的情况:
- 当随机变量相互独立时 , 一个随机变量的确定不会影响到另一个随机变量 ,
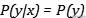 文章插图
文章插图- , 那么将会得到
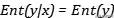 文章插图
文章插图- 。
- 当随机变量完全依赖时 , 一个随机变量的确定会使得另一个随机变量也确定下来 ,
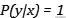 文章插图
文章插图- , 那么会得到
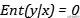 文章插图
文章插图- 。
- 启动|饿了么宣布启动“1212超级粉丝狂欢节”联合34家品牌推吃货卡季卡
- 自动驾驶汽车|海外|自动驾驶无法可依?美国多个团体联合发布自动驾驶立法大纲
- 展开|天地在线联合腾讯广告在京展开“附近推” 构建黄金5公里营销体系
- 合并|Andre Cronje主导批量「合并」DeFi项目,是好事情吗?
- 贬损|直播中贬损他人 快手联合西宁网信办处置青海四头部主播
- mini|电影、mini 与「当日完稿」工作流
- 字化转型|疫情重构经济,传统企业「数字化」的通关密码是什么?
- iPhone12|iPhone12「超大杯」拍照解禁:与Pro拉不开差距
- 演艺|中演院线与赋娱科技联合发布“智慧演艺”新业态
- 供应链|一座快手「重镇」的货端升级
