数学|逻辑的极限与数学的困境，罗素用了362页才推导出1+1=2 机器

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

为什么自亚里士多德以来的25个世纪里，直觉没有得到像逻辑那样多的关注？直觉是难以捉摸的，难以定义和量化，有时还具有欺骗性。事实上，甚至还有不同种类的直觉。亚里士多德认为，直觉是照亮黑暗的灯塔。然而，在黑暗中的大多数时间，它也像一个探照灯指向错误的方向。另一方面，逻辑可以被严格地证明，是精确和确定的。
庞加莱：用逻辑来演示，用直觉来发明

亨利·庞加莱， 1854 - 1921

亨利·庞加莱，法国数学家和物理学家，认识到我们的直觉可能有误导性（但主要负责数学的发展），逻辑推理是为了直观结果的最终论证。他把伟大的数学家分为两类，一类是遵循逻辑但不能“观察空间”的分析家，另一类是遵循直觉的几何学家，据庞加莱：

逻辑是证明的工具，只有它才能给出确定性；直觉是发明的工具（庞加莱， 1969）。

想象一下，在一节初等几何课上，有一个叫小明的学生，她用直觉和逻辑学习几何。直觉被用来寻找证明策略。然后用逻辑一步一步地建立一个证明。小明遇到了以下问题：

已知三角形ABC ，证明角a、角b、角c的和为180度。

小明马上想起了平角是180度。因此，他认为，这个问题一定和一条直线有关。但现在没有直线，那么就在某处画一条直线（辅助线）。试试在其中一个顶点处画一条直线，随便选c ，这条线应该是什么方向的？一个显而易见的选择是让它平行于AB 。通过辅助线，小明发现角a和角d是相等的，角b和角e是相等的，但这只是直观感受。但是，小明确实记得平行假设中的一些东西，它们确实相等，因此a + b + c = e + d + c = 180 。
在这一点上，他解决这个问题的所有想法都来自于猜测和自发的判断，这些都来自于他在课堂上所学到的知识。与其说他是一个逻辑推理者，不如说他是一个凭直觉进行猜测的人。接下来，她将运用自己的逻辑推理能力将这些点连接起来，并向她的几何老师演示一个证明。即使是这个简单的例子，小明也展示了一个典型的数学家是如何用直觉来发明和用逻辑来演示的。
罗素：不需要意义的游戏

伯特兰·罗素， 1872 - 1970

罗素和他的同事继续弗雷格未完成的研究（详细见：机器人之死——逻辑、直觉和悖论，决策者的困境?）。然而，数学家们越是努力避免弗雷格所反对的那种悖论，就越容易得出更微妙、更深刻的悖论。
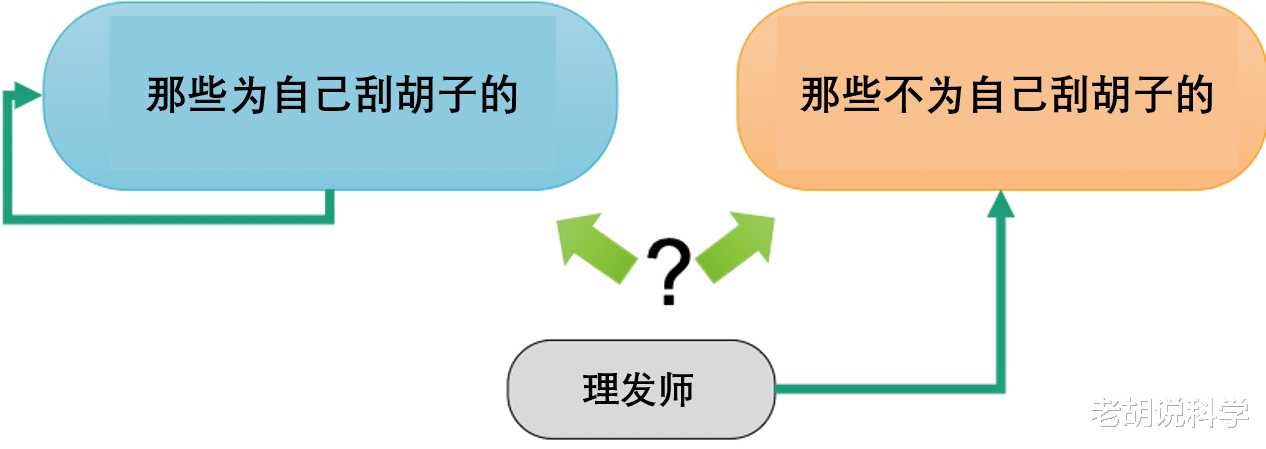
罗素给出了他的悖论的一个例证，叫做理发师悖论：

理发师会且只会为那些不给自己刮胡子的人刮胡子。理发师自己刮胡子吗？

如果理发师给自己刮胡子，他（这个理发师）就不给他刮胡子；这是一个矛盾。另一方面，如果理发师不给自己刮胡子，他就会被理发师刮胡子；这也是一个矛盾。
与弗雷格不同的是，罗素放弃了公理必须是不言而喻的这一观点，只要公理能够在不矛盾的情况下发展数学知识。他曾说过：