关键性|工程院院士孙凝晖：计算机系统的演进规律，从求极致到求通用

文章插图

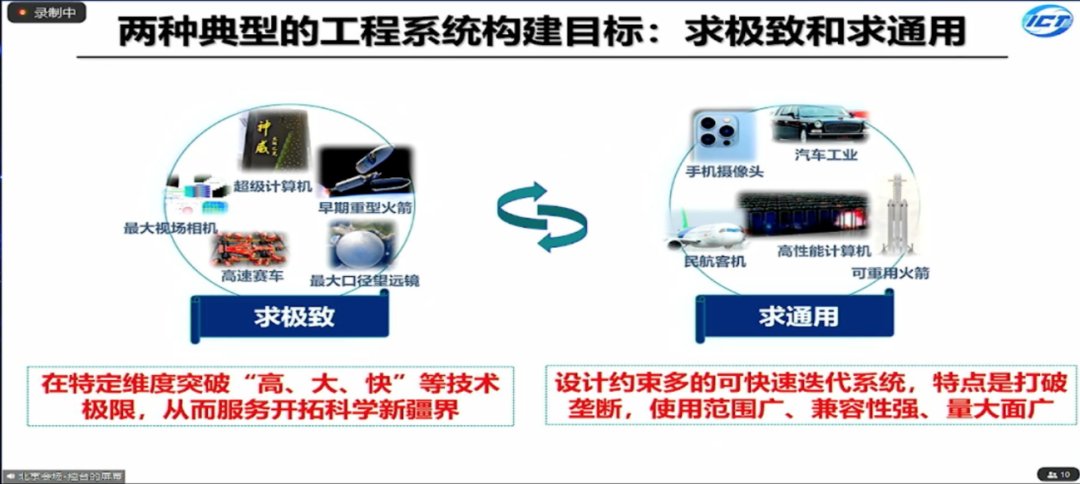
今天我想用这三大类方法来看一下计算机系统中的典型规律，我称它们为求极致的规律和求通用的规律。我们做大工程的系统建构主要有两个大目标，一个叫求极致，在特定维度或者核心技术上突破最高、最大、最快的技术极限，开拓科学研究的新疆界，比如，类似的工程有最快的超级计算机，最重的重型火箭，或者最大口径的望远镜，这类系统通常在学术研究中比较普遍。
另一个叫求通用，这类系统的设计要求约束多，可快速迭代，使用范围广，可兼容性强，比如我们的手机摄像头，汽车工业，民航客机，高性能计算机，这些都是求通用的典型系统，一般工业界对类似系统的建构更感兴趣。这两类系统在相互促进和相互转换的过程中，也存在一些内在规律。

文章插图

我举两个例子，一个求极致的例子是戴琼海院士在《自然-光子学（Nature Photonics）》杂志上发表的一项研究工作，这项研究将光学、微电子、计算机视觉以及信号处理等学科交叉，提出了一种显微成像新架构，研制了“实时超宽场高分辨率成像显微镜”，各项研究指标都达到了极致，比如1厘米x1.2厘米的超宽带视场，1.2微米的高分辨率，51亿像素每秒的数据通量。这一工作为生命科学和医学研究提供了一件“利器”。
另外一个求通用的例子是我们非常熟悉的手机成像技术，它不追求每一个单项指标都达到极致，而是用软硬一体化来补短板，占据除了专业相机以外的市场。它通过图像信号处理器（ ISP）弥补硬件在单项指标上的不足，让成像器件，图像计算硬件和处理软件协同进步，并通过快速迭代实现性能提升。
我简单总结了一下这两类系统建构的一些基本方法。
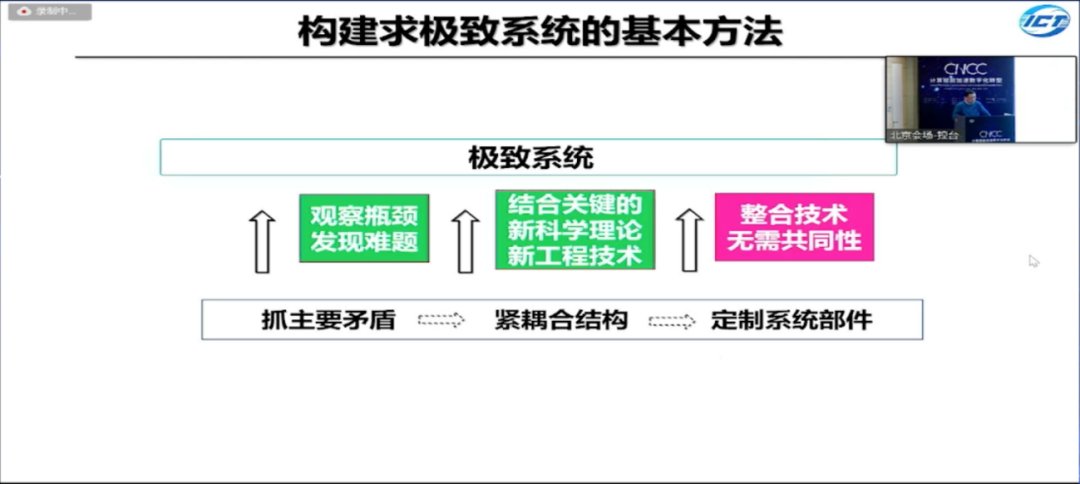
求极致的关键是抓主要矛盾，再结合关键的科学理论和工程技术突破指标上的极致，形成紧耦合结构，最后整合所有技术，定制系统内部需要的部件。

文章插图

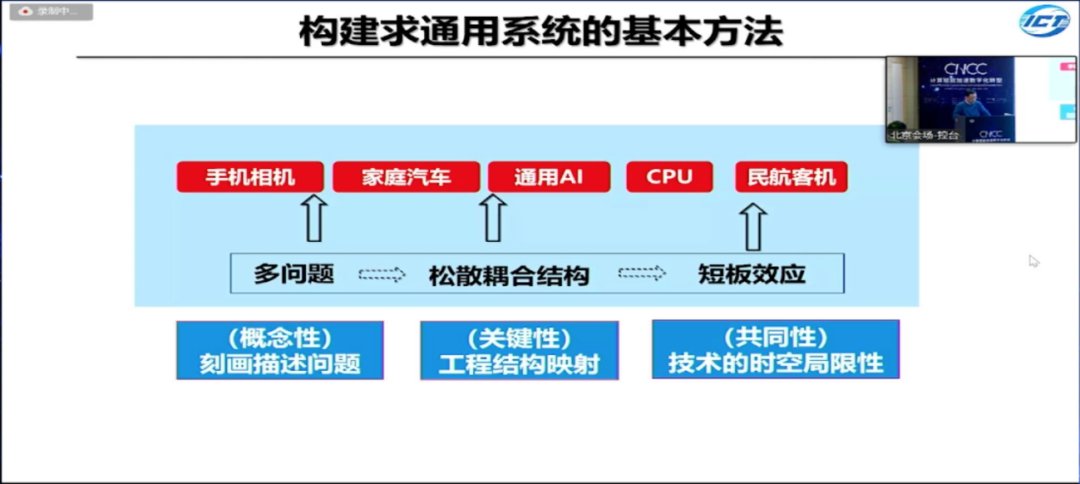
求通用系统在概念性上是一个多问题，需要对多个问题进行刻画和描述；在结构上通常是松散耦合的，需要对工程结构做最优映射；在共同性上要克服短板，解决技术的时空局限性等问题。

文章插图

从算盘、电子计算机走向HPC的繁荣之路

接下来，我首先回顾一下计算系统的发展历程。从工程科学的规律的角度，我们把视角拉远一些，我们观察到这样一条曲线，从最早的算盘，发展到电子计算机，再到现在的高性能计算机，中间出现了三个顶峰，三个山坡。这三个顶峰分别代表机械计算工具、超级计算机和未来Z级计算机。比如我们最早的算盘，爬到了机械计算工具的顶峰，因为有了一些规律，走到了通用计算机的繁荣。但这些系统在演化的过程中，究竟需要什么样的规律？这是我们需要思考的。

关键性|工程院院士孙凝晖：计算机系统的演进规律，从求极致到求通用｜CNCC 2021

文章插图

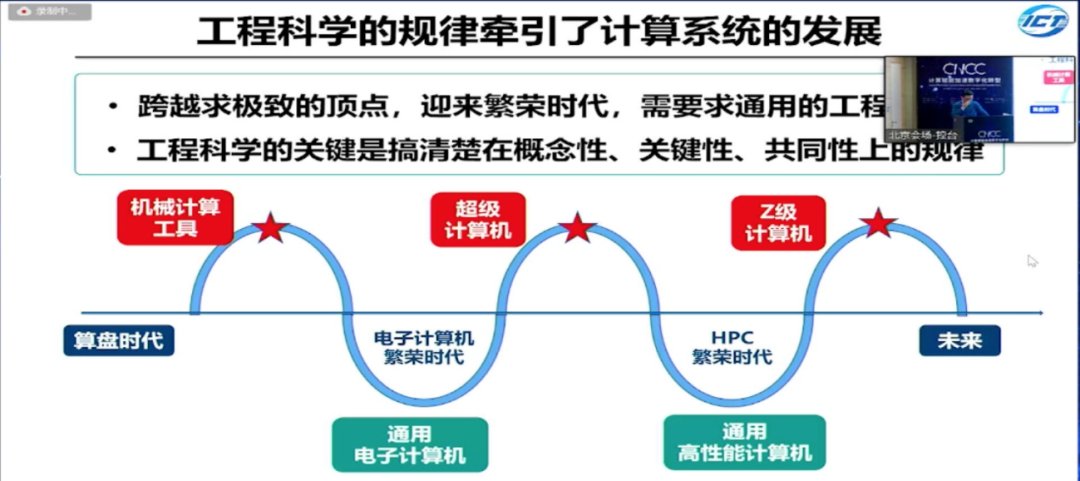
我先来介绍第一个曲线，这是一个历史的回顾，我们如何从算盘发展到通用的电子计算机。

如果做一个简单的罗列，人类历史上第一个人造计算工具诞生于中国公元1200年前，在它出现之前，我们只有数学（算术），没有Computing（计算）的概念。
第二步，帕斯卡和莱布尼兹发明了机械式加法器（1642）和乘法自动计算机（1673）。
第三步，1801年，杰卡德发明了首个可编程织布机——通过穿孔卡对织布机进行编程。
第四步，1837年，巴贝奇设计了差分机与分析机，虽然在工程上没有彻底实现，但已经可以完成非常复杂的计算，比如通过多项式逼近对数、指数和三角函数。
第五步，1843年，世界上第一位程序员爱达设计了一个算法，用来计算伯努利数列的值。这是第一个利用计算机进行运算的算法程序。
第六步，机械计算工具到了顶峰。二战期间，图灵为了破译密码设计出“图灵甜点”解码机。

至此机械式计算工具达到了工程技术积累的巅峰，直到出现了三位伟大学者，他们的发明奠定了现代通用计算机工程科学的三大基石，分别是：

关键性|工程院院士孙凝晖：计算机系统的演进规律，从求极致到求通用｜CNCC 2021( 二 )