算法|最强通用棋类AI，AlphaZero强化学习算法解读( 四 ) 算法|解读|ai|国际象棋|强化|棋

进行N次MCTS模拟
一次MCTS模拟从当前的棋盘状态出发，沿着博弈树中具有最大“置信区间上界（UCB）”值（后文会给出定义）的节点不断向下追溯，直到遇到之前从未见过的棋盘状态，也叫做“叶子”状态。这就是原论文中Part A所谓的“选择（Select）”。
置信区间上界是什么呢？用数学形式来说就是 Q(s, a) U(s, a)。其中 s 是状态，a 是走法。Q(s, a) 是我们希望由走法“a”构成状态“s”能够获得的期望值，与Q-Learning中的期望值一致。记住了，在这种情况下，该值的范围是-1（输）到1（赢）。U(s, a) ∝ P(s, a) / (1N(s, a))。这意味着U正比于P和N。其中，P(s, a) 是元组 (s, a) 的先验概率值，这个值是从神经网络那里得到的，而 N(s, a) 是已经访问过状态 s 与对应的走法 a 的次数。
# Upper Confidence Bounducb = Qsa[(s,a)]Ps[s,a] * sqrt(Ns[s]) / (1Nsa[(s,a)]
UCB的要点在于，其起初更倾向于具有较高先验概率（P）和较低访问次数（N）的走法，但渐渐地会倾向于具有较高动作价值（Q）的走法。
你不妨看看这里的代码好好理解一下。
# https://github.com/suragnair/alpha-zero-general/blob/5156c7fd1d2f3e5fefe732a4b2e0ffc5b272f819/MCTS.py#L105-L121cur_best = -float('inf')best_act = -1# pick the action with the highest upper confidence boundfor a in range(self.game.getActionSize()):if valids[a]:if (s, a) in self.Qsa:u = self.Qsa[(s, a)]self.args.cpuct * self.Ps[s][a] * math.sqrt(self.Ns[s]) / (1self.Nsa[(s, a)])else:u = self.args.cpuct * self.Ps[s][a] * math.sqrt(self.Ns[s]EPS)# Q = 0 ?if u > cur_best:cur_best = ubest_act = aa = best_actnext_s, next_player = self.game.getNextState(canonicalBoard, 1, a)next_s = self.game.getCanonicalForm(next_s, next_player)# Recursively visit the nodev = self.search(next_s)
Part A——选择具有最高置信区间上界值的走法
一旦找到一个叶子状态，就把这个棋面状态送入神经网络。这是论文中称作的Part B，“扩展与评估”。且看代码。
# leaf nodeself.Ps[s], v = self.nnet.predict(canonicalBoard)valids = self.game.getValidMoves(canonicalBoard, 1)self.Ps[s] = self.Ps[s] * valids# masking invalid movessum_Ps_s = np.sum(self.Ps[s])self.Ps[s] /= sum_Ps_s# renormalizeself.Vs[s] = validsself.Ns[s] = 0
Part B——扩展与评估
最后，我们将传回神经网络返回的值。这就是论文所说的Part C——“备份”。您可以在此处看到相关代码。
v = self.search(next_s)if (s, a) in self.Qsa:self.Qsa[(s, a)] = (self.Nsa[(s, a)] * self.Qsa[(s, a)]v) / (self.Nsa[(s, a)]1)self.Nsa[(s, a)]= 1else:self.Qsa[(s, a)] = vself.Nsa[(s, a)] = 1self.Ns[s]= 1return -v
Part C——备份
决定下一步如何走
让我们来看看AlphaZero面对上文提及的棋面时会决定如何走。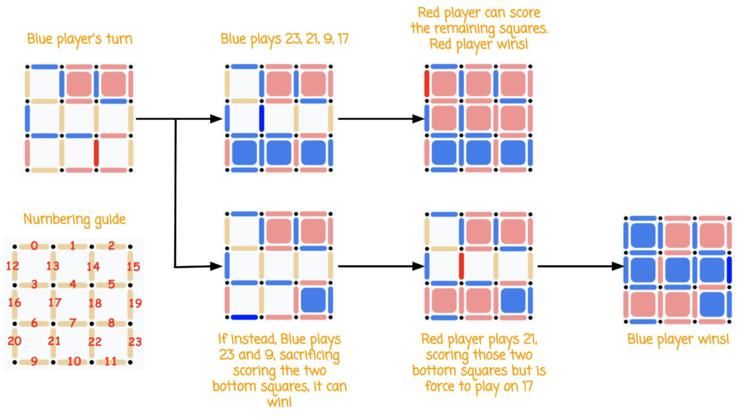

文章插图
AlphaZero会进行50次蒙特卡洛树搜索模拟。
你可以用这个在线notebook复现下面展示的结果。
下面展示的就是每次迭代的路径：
Simulation #1 -> Expand root nodeSimulation #2 -> 23Simulation #3 -> 21Simulation #4 -> 9Simulation #5 -> 17Simulation #6 -> 12Simulation #7 -> 19Simulation #8 -> 3Simulation #9 -> 18Simulation #10 -> 23,24Simulation #11 -> 21,24Simulation #12 -> 23,24,21Simulation #13 -> 21,24,23,24Simulation #14 -> 23,24,9Simulation #15 -> 23,24,17Simulation #16 -> 21,24,9Simulation #17 -> 23,24,12Simulation #18 -> 23,24,18Simulation #19 -> 21,24,17Simulation #20 -> 23,24,21,24,9Simulation #21 -> 21,24,19Simulation #22 -> 23,24,3Simulation #23 -> 21,24,18Simulation #24 -> 23,24,19Simulation #25 -> 21,24,23,24,17Simulation #26 -> 23,24,21,24,18Simulation #27 -> 23,24,21,24,3Simulation #28 -> 21,24,3Simulation #29 -> 23,24,21,24,19Simulation #30 -> 21,24,12Simulation #31 -> 23,24,21,24,9,24Simulation #32 -> 21,24,23,24,12Simulation #33 -> 23,24,21,24,9,24,18Simulation #34 -> 21,24,23,24,9,24,17Simulation #35 -> 23,24,21,24,9,24,12Simulation #36 -> 23,24,21,24,9,24,3Simulation #37 -> 21,24,23,24,9,24,19Simulation #38 -> 23,24,21,24,9,24,18,17Simulation #39 -> 21,24,23,24,9,24,18,17,24Simulation #40 -> 23,24,21,24,9,24,18,17,24,19Simulation #41 -> 21,24,23,24,9,24,18,17,24,19,24Simulation #42 -> 23,24,9,21Simulation #43 -> 23,24,9,18Simulation #44 -> 23,24,9,17Simulation #45 -> 23,24,9,19Simulation #46 -> 23,24,9,12Simulation #47 -> 23,24,9,21,24Simulation #48 -> 23,24,9,3Simulation #49 -> 23,24,9,21,24,18Simulation #50 -> 23,24,9,21,24,17
上面显示的结果的意思是：在第一次模拟中，由于算法之前并未见过这个棋面，因此输入的棋面实际上是一个“叶子”状态节点，需要先“扩展”这个节点。所谓扩展就是把棋面送到神经网络里对每个位置进行概率评估。
Simulation #1 -> Expand root node