算法|最强通用棋类AI，AlphaZero强化学习算法解读( 三 ) 算法|解读|ai|国际象棋|强化|棋

文章插图
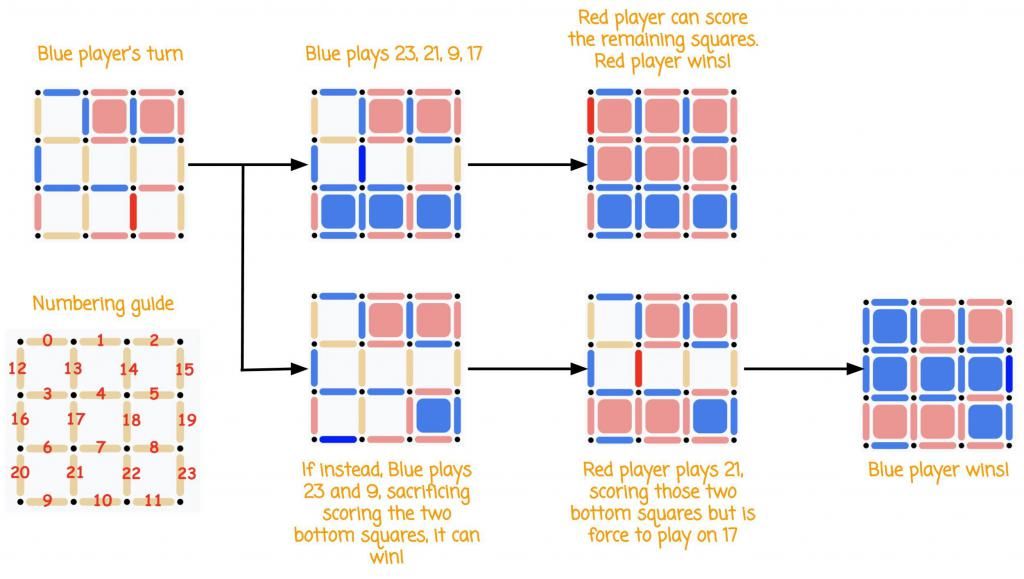
（译者注：左下角是每根线的编号。如果你刚刚已经在网页上跟AlphaZero玩过这个游戏了，那么相信这张图是很容易理解的。上方第一种走法只顾眼前短期利益，最终葬送好局。）
如果蓝色方走23再走21，那么红色方必赢。然而，如果蓝色方走23后再走9，那蓝色方就赢了。要是AlphaZero在蓝色方，它怎么知道哪一种走法能够赢下来呢？
你可以用这个在线notebook复现我们即将呈现的效果。
将棋面送入神经网络，我们就能得到下一步走在不同位置的概率：
move_probability[0]: 9.060527501880689e-12move_probability[1]: 3.9901679182996475e-10move_probability[2]: 3.0028431828490586e-15move_probability[3]: 7.959351400188552e-09move_probability[4]: 5.271672681717021e-11move_probability[5]: 4.101417122592821e-12move_probability[6]: 1.2123925357696643e-16move_probability[7]: 6.445387395019553e-23move_probability[8]: 2.8522254313207743e-22move_probability[9]: 0.0002768792328424752move_probability[10]: 1.179791128073232e-13move_probability[11]: 5.543385303737047e-13move_probability[12]: 3.2618200407341646e-07move_probability[13]: 4.302984970292259e-14move_probability[14]: 2.7477634988877216e-16move_probability[15]: 1.3767548163795204e-14move_probability[16]: 8.998188305575638e-11move_probability[17]: 7.494002147723222e-07move_probability[18]: 8.540691764924446e-11move_probability[19]: 9.55116696843561e-09move_probability[20]: 4.6348909953086714e-12move_probability[21]: 0.46076449751853943move_probability[22]: 2.179317506813483e-20move_probability[23]: 0.5389575362205505move_probability[24]: 5.8165523789057046e-15
同时，我们还能得到当前棋局的赢面有多大：
-0.99761635
你可以在这里查阅与这些输出相关的代码。
这些输出值有一些很有意思的地方，我们来细品一下：
在所有可能画线的位置，23号、21号以及9号的概率值最大。如果神经网络选择在23号以及21号位置处画线，那么它就能够得到1分。另外，23号才是能够赢下来的走法，而相应地，从网络输出的概率来看，23号位置的概率（0.53）恰好比21号的（0.46）稍微高一点儿。
神经网络也会给不能够画线的位置输出一个概率值。虽然如此，但是代码上还是要进行限制，以确保计算机不会在不合规则的位置画线。
棋面的输赢概率为-0.99。这意味着AlphaZero认为它已经输掉游戏了。这个概率值的范围是-1（输）到1（赢）。这个值本应该很接近于1（赢）而不是-1（输）的，毕竟我们知道目前这个局面赢面很大。也许我们应该多训练几轮来让AlphaZero准确预估棋面的输赢概率。
我们很容易利用神经网络的输出来决定下一步的走法。
在棋盘游戏中（现实生活中也是），玩家在决定下一步怎么走的时候往往会“多想几步”。AlphaZero也一样。我们用神经网络来选择最佳的下一步走法后，其余低概率的位置就被忽略掉了。像Minimax这一类传统的AI博弈树搜索算法效率都很低，因为这些算法在做出最终选择前需要穷尽每一种走法。即使是带有较少分支因子的游戏也会使其博弈搜索空间变得像是脱缰的野马似的难以驾驭。分支因子就是所有可能的走法的数量。这个数量会随着游戏的进行不断变化。因此，你可以试着计算一个平均分支因子数，国际象棋的平均分支因子是35，而围棋则是250。
这意味着，在国际象棋中，仅走两步就有1,225（352）种可能的棋面，而在围棋中，这个数字会变成62,500（2502）。在Dots and Boxes游戏中，对于一个3×3大小的棋盘，初始的分支因子数是24，随着棋盘不断被填充，这个数字会不断减少（除非空过）。所以，在行至中局，分支因子变为15的时候，仅走3步就会有多达2730（15*14*13）种可能的棋面。
现在，时代变了，神经网络将指导并告诉我们哪些博弈路径值得探索，从而避免被许多无用的搜索路径所淹没。现在神经网络告诉我们23号和21号都是非常值得一探究竟的走法。
接着，蒙特卡洛树搜索算法就将登场啦！
蒙特卡洛树搜索（MCTS）
神经网络为我们指示了下一步可能的走法。蒙特卡洛树搜索算法将帮助我们遍历这些节点来最终选择下一步的走法。
去这个链接看看论文中有关蒙特卡洛树搜索的图形化描述。
使用MCTS的具体做法是这样的，给定一个棋面，MCTS共进行N次模拟。N是模型的超参数。N次模拟结束后，下一步的走法将是这N次模拟中所经次数最多的一步。你可以由这里的代码一窥究竟：
# https://github.com/suragnair/alpha-zero-general/blob/5156c7fd1d2f3e5fefe732a4b2e0ffc5b272f819/MCTS.py#L37-L48for i in range(self.args.numMCTSSims):# self.args.numMCTSSims, the number of MCTS simulations to computeself.search(canonicalBoard)# "search" is a MCTS simulationss = self.game.stringRepresentation(canonicalBoard)# Count how many times we have visited each nodecounts = [self.Nsa[(s, a)] if (s, a) in self.Nsa else 0 for a in range(self.game.getActionSize())]if temp == 0:# Pick the node that was visited the mostbestAs = np.array(np.argwhere(counts == np.max(counts))).flatten()bestA = np.random.choice(bestAs)probs = [0] * len(counts)probs[bestA] = 1return probs