专治|专治各种不明白，一文带你了解“对抗样本原理”( 二 ) 中薪|高薪|样本|原理|对抗|一文

文章插图
图4 线性分类数据集

文章插图
图5 线性分类的等高线图
在图5中，线条表示神经网络模型y=f(x)的等高线。根据等高线的密集程度，可以将二维平面分为不稳定区域和稳定区域。
不稳定区域：等高线密集的区域。在不稳定区域中，y=f(x)的梯度的绝对值较大，即函数值y随着x变化较快，x的微小变化会对y的值造成大的影响。
稳定区域：等高线稀疏的区域。在稳定区域中，函数值y随着x变化较慢，x的微小变化不会对y的值造成大的影响。
如图 5所示，如果输入数据落在神经网络模型的不稳定区域中，那么该模型在这个输入数据处容易被对抗样本欺骗。如果输入数据落在神经网络模型的稳定区域中，那么该模型在这个输入数据处就不容易被对抗样本欺骗。这就解释了在实际的神经网络模型中，例如图像识别的神经网络，某些输入图像经过微小的改动就能够使模型分类错误，而另一些图像即使经过较大的改动仍然可以使模型输出正确的分类结果。
另外，由梯度的定义可知，梯度向量与等高线是正交的。沿着梯度的方向函数值变化最快，而沿着等高线的方向，函数值不发生变化。因此对于落在不稳定区域的输入数据x来说，其对扰动?x的敏感程度取决?x与梯度向量（或等高线）的夹角。若?x沿着梯度方向，那么微小的‖?x‖就会使模型函数的输出y发生大的变化。如果?x沿着等高线方向，那么即使‖?x‖较大，函数的输出y也不会发生变化。这就解释了在实际的神经网络模型中，例如用于图像识别的神经网络，一些图像只有经过特定的扰动才会引起分类错误，而并不是针对图像的任何扰动都会引起分类错误。
双半月数据集的二分类问题
前面通过等高线分布图说明了对抗样本的作用机理。下面针对更加复杂的数据集来进一步展示。本节对双半月形数据集进行二分类。数据集和神经网络的等高线图分别如图6和图7所示。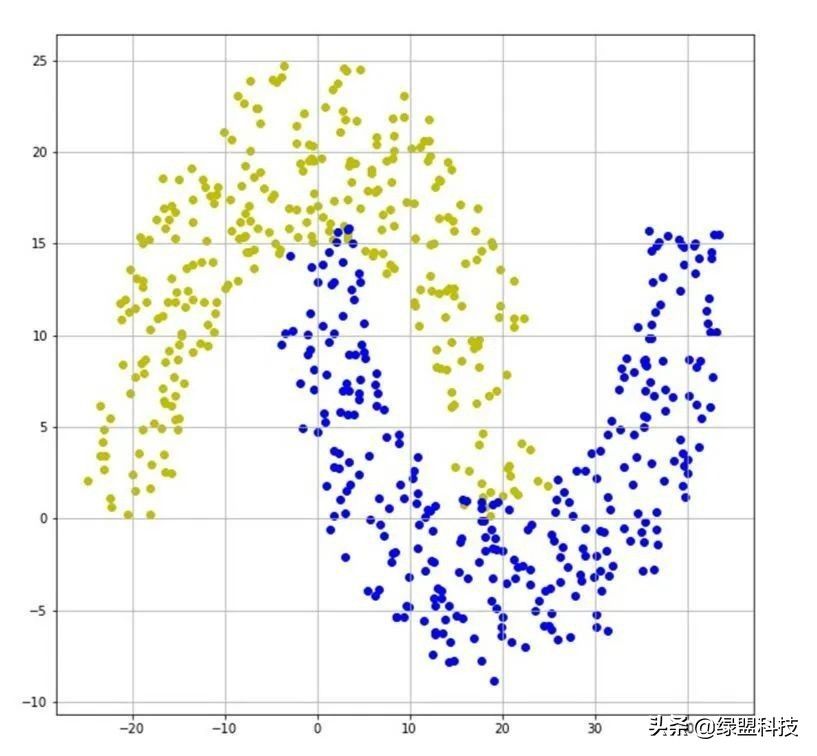

文章插图
图 6 双半月形数据集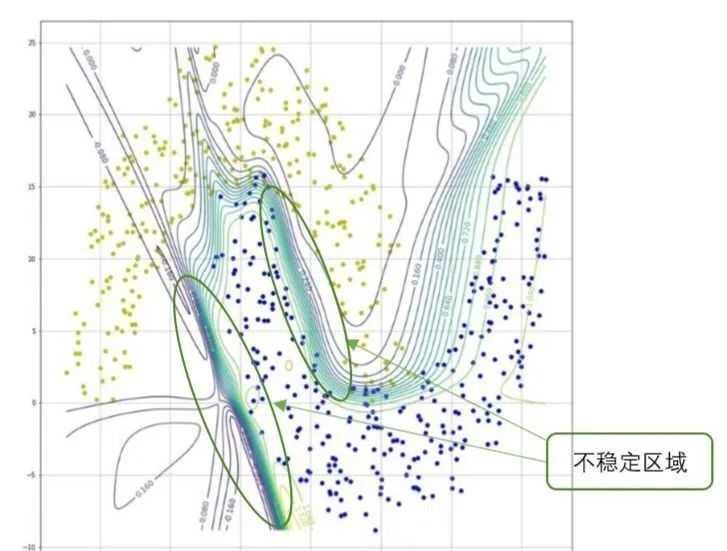

文章插图
图7 双半月形数据集的等高线图
对于双半月形数据集，其分类模型函数的等高线分布更加复杂。在图6可以看出，两类数据之间的距离较近，同时还有部分交叉，因此决策边界处的等高线较密集。与线性分类相似，在等高线密集的区域，如果输入量x沿着梯度的方向发生微小的变动，那么就会导致模型的输出y发生较大的变化。
环形数据集
环形数据集和其神经网络的等高线图分别如图8和图9所示。

文章插图
图8 环形数据集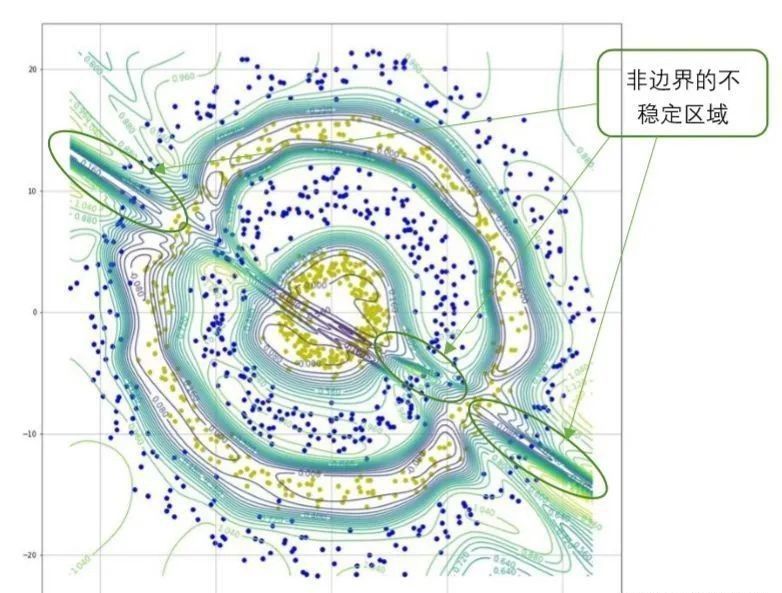

文章插图
图9 环形数据集的等高线图
图8所示的数据集中的两类数据同样距离较近，且有部分交叉。从图9可以看出，等高线更加复杂，不稳定区域也更多。由于两类数据的距离较近，因此决策边界处属于不稳定区域。同时，在非边界处也出现了等高线密集的区域。也就是说在非决策边界处也出现了不稳定区域，如图9中所示。在这些不稳定区域中，模型容易被对抗样本所欺骗。可见，对于复杂分布的数据集来说，模型的不稳定区域更多，分布也更加复杂。
四、总结以上通过不同的数据集展示了神经网络模型被对抗样本欺骗的原理。为了方便说明，以上数据集中的数据都为二维，可以直观的通过图像来展示。随着数据集中的数据分布越来越复杂，模型的不稳定区域会更多，同时不稳定区域的位置也更加难以预测。在实际应用中，数据集的维度往往非常高，例如MNIST数据集每个样本有784个特征，即784维；CIFAR数据集每个样本有3072个特征，即3072维。对于高维的数据空间，其数据的分布往往不可知，且模型的决策边界更加复杂，无法通过图像来直观的展示，因此无法准确地知道模型不稳定区域的分布。目前学术界虽然提出了一些对抗攻击的防护方法，但效果都有限，其主要原因就在于目前已有的研究主要是通过各种方法改变了不稳定区域的位置，但并没有将其消除。对于高维数据集和更加复杂的分类模型来说，其模型的不稳定区域的分布不可预知。因此，对抗样本的防护问题现在并没有从根本上被解决，还需要从数学原理上进行更加深入的研究。