15张图来了解「树」，面试再也不怕被刷了( 二 ) 树的概念什么是树？树属于非

//创建树--插入数据void insert(Tree* tree, int value){//创建一个节点，让左右指针全部指向空，数据为valueNode* node=(Node*)malloc(sizeof(Node));node->data = http://kandian.youth.cn/index/value;node->left = NULL;node->right = NULL;//判断树是不是空树，如果是，直接让树根指向这一个结点即可if (tree->root == NULL){tree->root = node;} else {//不是空树Node* temp = tree->root;//从树根开始while (temp != NULL){if (value < temp->data){ //小于就进左儿子if (temp->left == NULL){temp->left = node;return;} else {//继续往下搜寻temp = temp->left;}} else { //否则进右儿子if (temp->right == NULL){temp->right = node;return;}else {//继续往下搜寻temp = temp->right;}}}}return;}遍历，显示树代码如下：
//树的中序遍历 In-order traversalvoid inorder(Node* node){if (node != NULL){inorder(node->left);printf("%d ",node->data);inorder(node->right);}}树的遍历之先序遍历二叉树遍历简介遍历是按照一定的规则性，将数据结构中的所有数据全部依次访问，而二叉树需要通过在各节点与其孩子之间约定某种局部次序，间接地定义某种全局次序。

先序遍历：根左右

先序遍历：先序遍历就是在访问二叉树的结点的时候采用，先根，再左，再右的方式，对于一个最简单的访问而言如下图，先序遍历的访问顺序就是A ， B ， C

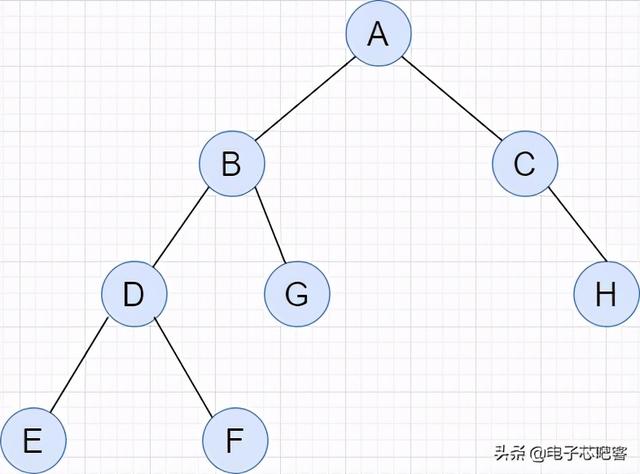
文章插图
多个结点相互嵌套构成的二叉树如图所示，在访问遍历一开始的时候，先访问根结点A ，次访问左节点B ，由于左结点中嵌套了一组结点，因此左节点又作为下一个结点的根结点。
继续沿着B访问到了D ，同样由于D中包含了一组新的结点， D又作为根节点继续访问，就又访问到了E ，由于E没有后面的结点了，作为D为根的左结点E访问结束后，访问到F ，这一组访问结束之后再回退访问G ，那么这一个二叉树的先序遍历访问顺序就是：ABDEFGCH

文章插图
代码实现

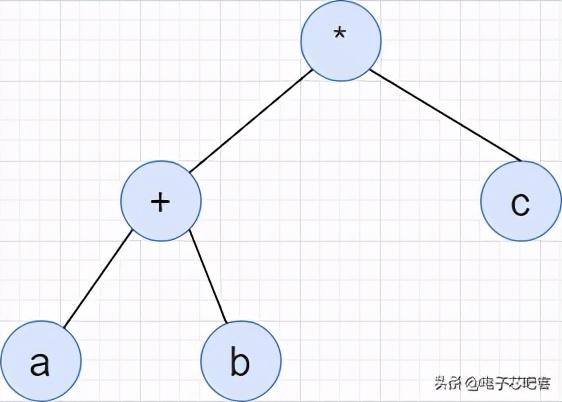
//树的先序遍历 Preorder traversalvoid preorder(Node* node){if (node != NULL){printf("%d ",node->data);inorder(node->left);inorder(node->right);}}

扩展->前缀表达式我们日常的运算表达式通常是如下形式，这种成为中缀表达式，也就是运算符在运算数的中间，如图，为常规表达式：(a+b)*c
其二叉树的表现形式为：

文章插图
而前缀表达式的表达方式就是 *+cab，它的一个特征就是符号迁移，常规的表达式是需要大量的括号表达先后顺序的，而这样的表达式表达形式不需要，更容易让计算机处理。
我们常规的表达式的计算是中序的，而计算机更方便对前缀表达式这样的方式进行理解，进行这样的转换首先思路要进行转换。
在代码中我们实现这样的转换一般可以利用栈，熟练书些这样的转换就需要STL的掌握。
树的遍历之中序遍历二叉树简介

中序遍历：左根右

如下图，就一个最简单的二叉树遍历而言，中序遍历的遍历访问过程是先B再A再C 。

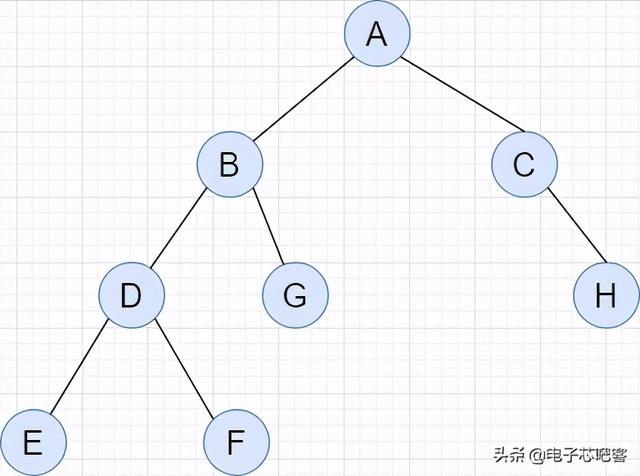
文章插图
多个结点构成的如图所示，进行第一次访问的时候，我们在ABC中进行遍历，由左根右的顺序，我们遍历访问到B ， B同时又作为BDG的根结点，因此需要继续向下进行遍历。
此时我们遍历到DEF ，这时E属于这一组之中的左结点，因此我们根据根左右的先后顺序得到了最先的遍历效果， EDF 。
这EDF同时作为BDG中的左节点（把EDF看作一个整体）进行回溯，此时的访问的结点顺序为EDFBG 。
同理EDFBG作为ABC的左结点根据左根右的顺序EDFBGAC ，左半部分访问完毕接着访问右半部分，我们将^CH（^表示空）看作一组左中右，而C就是由EDFBGAC组合而成，因此最终的遍历顺序为：EDFBGACH

文章插图
代码实现

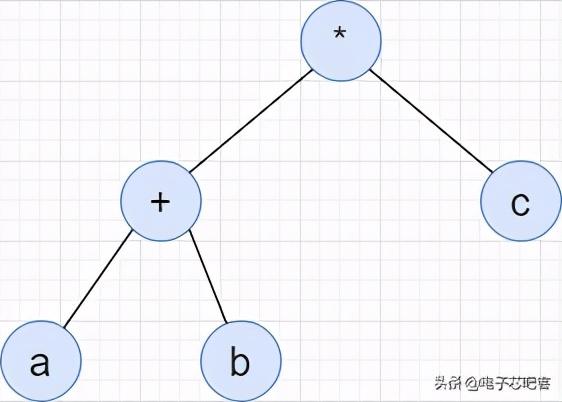
//树的中序遍历 In-order traversalvoid inorder(Node* node){if (node != NULL){inorder(node->left);printf("%d ",node->data);inorder(node->right);}}

中缀表达式（常规算式）中缀表达式是一个通用的算术或逻辑公式表示方法。中缀表达式就是我们最常用的表达式形式，也是人最容易理解的表达式形式。
如图，为常规表达式：(a+b)*c
其二叉树的表现形式为：

文章插图