15张图来了解「树」，面试再也不怕被刷了树的概念什么是树？树属于非

树的概念什么是树？树属于非线性数据结构的一种，概念也极多，是由结点或顶点和边组成的且不存在着任何环的一种数据结构。
没有结点的树称为空树。一棵非空的树包括一个根结点，还很可能有多个附加结点，并且所有结点构成一个多级分层结构。
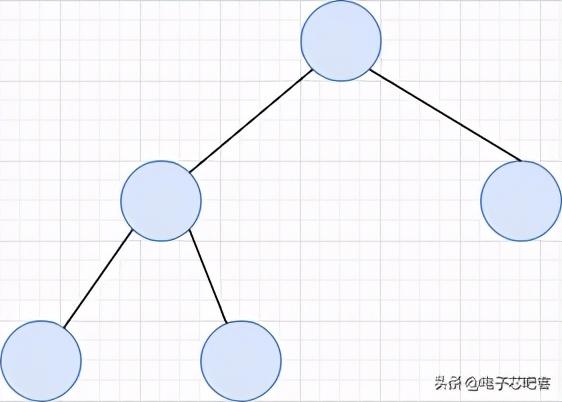
树的定义n个节点组成的有限集合。 n=0 ，空树；n>0,1个根节点， m个互不相交的有限集，每个子集为根的子树，如图所示为一颗树：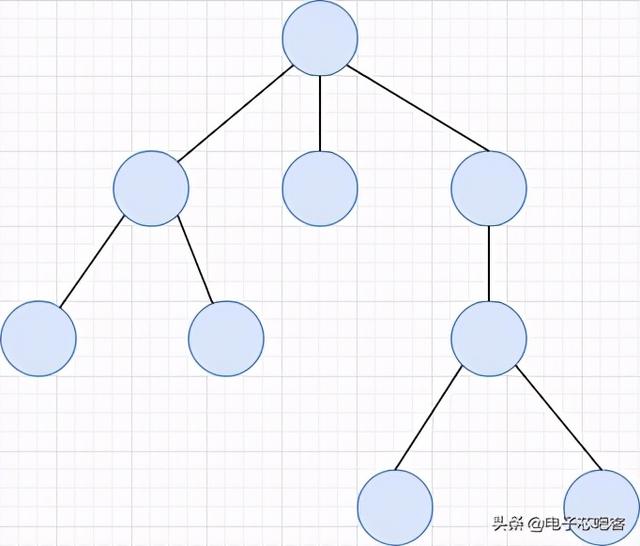
文章插图
树的基本术语

节点的度：树中某个节点的子树的个数。
树的度：树中各节点的度的最大值。
分支节点：度不为零的节点。
叶子节点：度为零的节点。
路径：i->j；
路径长度：路径经过节点数目减1 。
孩子节点：某节点的后继节点；
双亲节点：该节点为其孩子节点的双亲节点（父母节点）；
兄弟节点：同一双亲的孩子节点；
子孙节点：某节点所有子树中的节点；
祖先节点：从树节点到该节点的路径上的节点；
节点的层次：根节点为第一层，以此类推；
树的高度：树中节点的最大层次；
有序树：树中节点子树按次序从左向右安排，次序不能改变；
无序树：与有序树相反；
森林：互不相交的树的集合。

树的性质

树的节点树为所有节点度数加1（加根节点）。
度为m的树中第i层最多有m^(i-1)个节点。
高度为h的m次树至多(m^h-1)/(m-1)个节点。
具有n个节点的m次树的最小高度为logm( n(m-1) + 1 )向上取整。

二叉树二叉树简介二叉树是n(n>=0)个结点的有限集合，每一个结点中最多拥有一个左结点和一个右结点，并且没有多余的结点，如图所示：

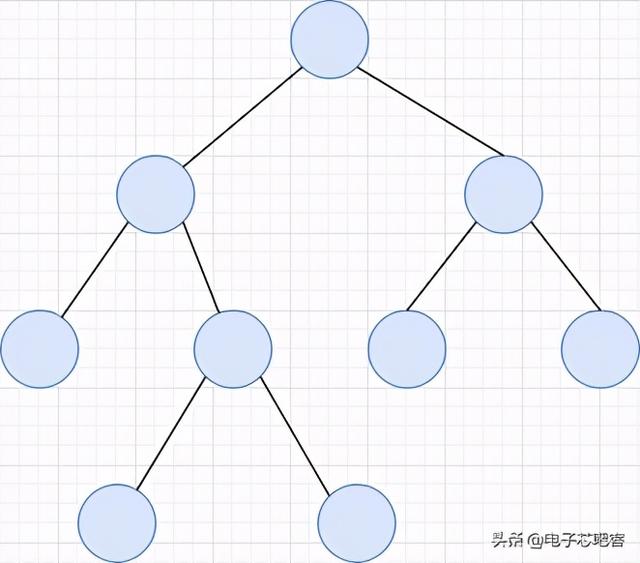文章插图
二叉树的特点根据二叉树的定义以及图示分析得出二叉树有以下特点：

每个结点最多有两颗子树，不存在度大于2的结点。
左子树和右子树的次序不能任意颠倒。
即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

二叉树的性质【15张图来了解「树」，面试再也不怕被刷了】二叉树具有以下几种特征

二叉树第i层上的结点数目最多为2{i-1} (i≥1) 。
深度为k的二叉树至多有(2{k}-1)(k≥1)个结点。
包含n个结点的二叉树的高度至少为log2 (n+1) 。
在任意一棵二叉树中，若终端结点的个数为n0 ，度为2的结点数为n2 ，则n0=n2+1 。

几种特殊的二叉树斜树所有的结点都只有左(右)子树的二叉树叫左(右)斜树，统称为斜树，如图所示：

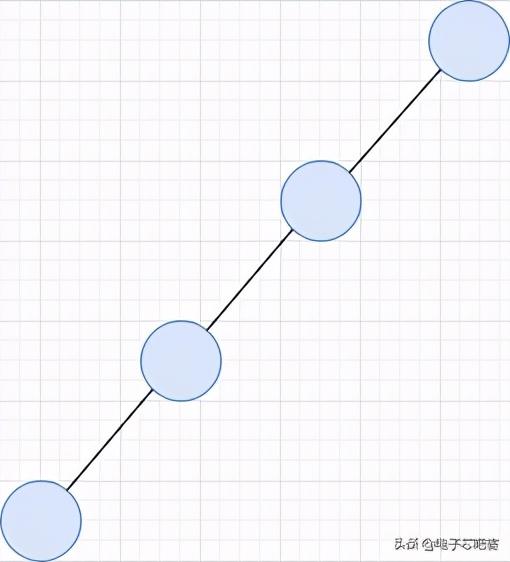文章插图
满二叉树在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树，其有以下特点

叶子只能出现在最下一层，否则就不可能达成平衡。
非叶子结点的度一定是2 。
在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

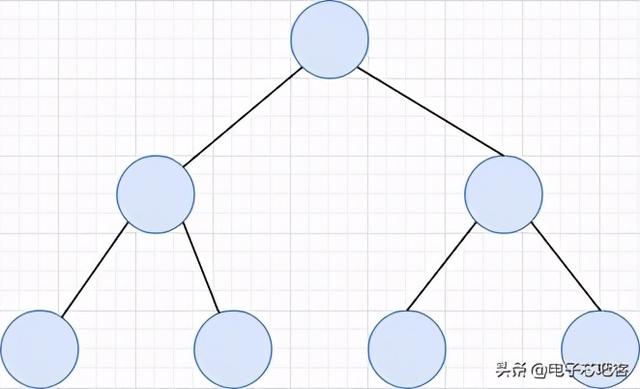文章插图
完全二叉树一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

文章插图
二叉树的存储简介以创建一颗二叉树，并实现通过特定的插入顺序和读取顺序达成读取为顺序为例子进行简介。
结点设计一颗二叉树的结点设计一定要有如下内容：

结点元素， data域，用来存储数据；
左孩子结点， left指针，用来指向当前结点的下一层的左边结点；
右孩子结点， right指针，用来指向当前结点的下一层的右边结点；

除此之外，我们使用一棵树的时候需要建立一颗树根，由这个根，来进行逐步的向下构建，其代码如下：

//树的结点typedef struct node{int data;struct node* left;struct node* right;} Node;//树根typedef struct {Node* root;} Tree;

树的创建首先创建一个空的结点进行连接，将这个空的结点中的date域赋予数据，再判断tree中是否是一个空树，如果为空，只需要将整个根指向这一个结点即可，如果不为空，再进行两个判断，判断输入的数据是否大于或者小于当前比对的结点数据，根据其大小进行相应的排列，这样存储进入的数据总是有一定规律的，在输出的时候根据这个规律进行输出即可，其代码可以显示为：