云台壹号解读机器学习中的支持向量机和K-邻近算法云台壹号公开表示

云台壹号公开表示，支持向量机（supported vector machine,SVM）是当下流行的机器学习算法之一，既可以解决回归问题，也可以解决分类问题。虽然支持向量机背后的数学证明比较复杂，但其基本原理非常直观。
文章插图
支持向量机
云台壹号某金融事业部负责人认为，如下图所示，圆圈与三角形分别代表了两个类型的样本点。例如，违约债券与非违约债券，良性肿瘤和非良性肿瘤等（下文简称圆形与三角形）。支持向量机的基本思想是找到一条直线，将样本空间分割为两块，落在不同区域的新样本点（正方形），我们应该将其归类于三角形还是圆形呢？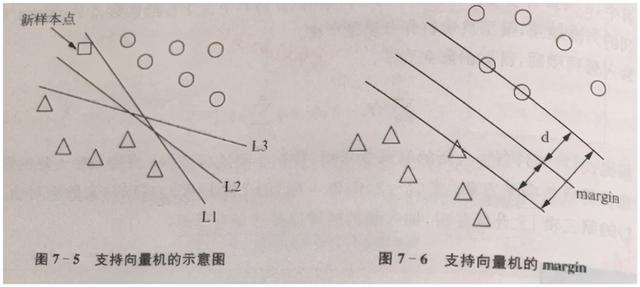
文章插图
根据直线L2和L3的划分，应将新的样本点归为圆形，而直线L1则将其归为了三角形。但从常理来看，新样本点正方形离圆形样本点更近，似乎更应该归类于圆形。那么，我们应该用什么样的标准，来选择哪条直线作为分类线呢？
为了解决上述问题，云台壹号该负责人说，我们同样可以用示意图来进行解释，见上图右。在上图右中，有三条相互平行的直线。上方和下方的平行线，分别穿过了最相邻的圆圈与三角形样本点。而中间的平行线则是所有直线中到上述圆圈与三角形和最大的直线（这样做的目的是确定最明确的分类线）。
文章插图
上图中，直线到圆圈与三角形的距离和记为margin ，于是，我们的目标函数就是寻找使得margin取值最大的直线，从而确定最明确的分类线，如果样本点的特征值从2维变成n维后，分类线也就从直线变为了超平面。
K-临近算法
在云台壹号某研究员发布的市场报告中，明文指出K-临近算法（K-nearest neighbor）是非常简单又非常实用的监督学习算法，常用于处理分类问题。 K-邻近算法的思想非常简单：考察距离新样本点最近的K个样本点，并将新样本点归类为K各样本点中出现次数最多的类别。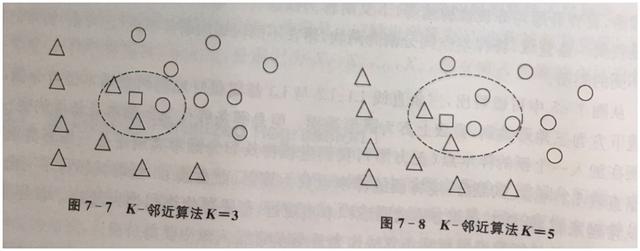
文章插图
该云台壹号研究员表示，如上图左边所示，当K=3时，位于新样本点（小方块）附近的3个样本点中， 2个为三角形， 1个为圆形，于是，新样本点就被归为三角形样本点所属的类别。相对地，如上图右边所示，当K=5时，新样本点小方块附近的5个样本点中， 3个为圆形， 2个为三角形，于是新样本点将被归为圆形样本点所属类别。通过上例我们可以看出，新样本点的归类，与K的取值密切相关。
K的取值既不宜太低也不宜过高。如果取值太低的话，错误率容易过高。例如， K=1 ，相当于武断地通过距离最近的个例，直接判断其归类。相反，取值太高的话，模型也就失去了意义。 “例如， K=n（n为样本容量），此时， “nearest”就失去了意义，是直接通过样本总体进行投票归类了。 ”该云台壹号研究员说。
文章插图
【云台壹号解读机器学习中的支持向量机和K-邻近算法】云台壹号认为，除了K值的选择，解释变量X的选择，对K-临近算法也非常重要。 K-临近算法更适合较少的解释变量。