【协方差矩阵|五步掌握主成分分析法：数据少少，信息多多！】本文的目的是为主成分分析（

按关键词阅读： 协方差矩阵 变量 数据集 协方差 PCA

协方差矩阵|五步掌握主成分分析法：数据少少，信息多多！文章插图
本文的目的是为主成分分析（PCA）提供一个完整且简单的解释，特别是其运作方式，以增进大家对该分析法的理解并加以利用，而不必具有强大的数学背景。
PCA实际上是网上广泛提及的一种方法，很多文章都有涉及。但是，只有极少数文章能直接切入主题，并在不过多钻研技术细节的前提下解释PCA的工作原理以及“为什么” 。这就是这篇文章的目的：以更简单的方式解释主成分分析法。
在开始解释之前，本文提供了PCA在每一步骤的运作原理的逻辑解释，简化了其背后的数学概念，如标准化，协方差，特征向量和特征值，而暂未关注如何运算的问题。
协方差矩阵|五步掌握主成分分析法：数据少少，信息多多！文章插图
什么是PCA？
PCA是一种常用于减少大数据集维数的降维方法，把大变量集转换为仍包含大变量集中大部分信息的较小变量集。
减少数据集的变量数量，自然是以牺牲精度为代价的，降维的好处是以略低的精度换取简便。因为较小的数据集更易于探索和可视化，并且使机器学习算法更容易和更快地分析数据，而不需处理无关变量。
总而言之， PCA的概念很简单——减少数据集的变量数量，同时保留尽可能多的信息。
协方差矩阵|五步掌握主成分分析法：数据少少，信息多多！文章插图
逐步解释
第1步：标准化
这一步的目的是把输入数据集变量的范围标准化，以使它们中的每一个均可大致成比例地分析。
更具体地说，在使用PCA之前必须标准化数据的原因是PCA对初始变量的方差非常敏感。也就是说，如果初始变量的范围之间存在较大差异，那么范围较大的变量将占据范围较小的变量（例如，范围介于0和100之间的变量将占据0到1之间的变量），这将导致主成分的偏差。因此，将数据转换为可比较的比例可避免此问题。
在数学上，这一步可以通过减去平均值，再除以每个变量值的标准偏差来完成。
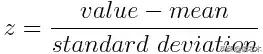协方差矩阵|五步掌握主成分分析法：数据少少，信息多多！文章插图
只要标准化完成后，所有变量都将转换为相同的范围[0,1] 。
第2步：协方差矩阵计算
这一步的目的是：了解输入数据集的变量是如何相对于平均值变化的。或者换句话说，是为了查看它们之间是否存在任何关系。因为有时候，变量间高度相关是因为它们包含大量的信息。因此，为了识别这些相关性，我们进行协方差矩阵计算。
协方差矩阵是p×p对称矩阵（其中p是维数），其所有可能的初始变量与相关联的协方差作为条目。例如，对于具有3个变量x ， y和z的三维数据集，协方差矩阵是以下的3×3矩阵：
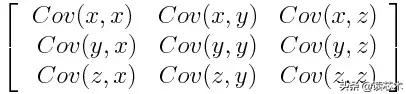协方差矩阵|五步掌握主成分分析法：数据少少，信息多多！文章插图
由于变量与其自身的协方差是其方差（Cov（a ， a）= Var（a）），因此在主对角线（左上角到右下角）中，实际上有每个起始变量的方差。并且由于协方差是可交换的（Cov（a ， b）= Cov（b ， a）），协方差矩阵的条目相对于主对角线是对称的，这意味着上三角形部分和下三角形部分是相等的。
作为矩阵条目的协方差告诉我们变量之间的相关性是什么呢？
协方差的重要标志如下：
· 如果为正，则两个变量同时增加或减少（相关）
· 如果为负，则一个减少，另一个增加（不相关）
好了，现在我们知道协方差矩阵只不过是一个表，汇总了所有可能配对的变量间相关性。让我们继续下一步。
第3步：计算协方差矩阵的特征向量和特征值，用以识别主成分
特征向量和特征值都是线性代数概念，需要从协方差矩阵计算得出，以便确定数据的主成分。开始解释这些概念之前，让我们首先理解主成分的含义。
主成分是由初始变量的线性组合或混合构成的新变量。该组合中新变量（如主成分）之间彼此不相关，且大部分初始变量都被压缩进首个成分中。所以， 10维数据会显示10个主成分，但是PCA试图在第一个成分中得到尽可能多的信息，然后在第二个成分中得到尽可能多的剩余信息，以此类推。
例如，假设你有一个10维数据，你最终将得到的内容如下面的屏幕图所示，其中第一个主成分包含原始数据集的大部分信息，而最后一个主成分只包含其中的很少部分。因此，以这种方式组织信息，可以在不丢失太多信息的情况下减少维度，而这需要丢弃携带较少信息的成分。