【一文看懂如何使用（Py）Stan进行贝叶斯推理】在PyStan中应用贝叶斯回归鼓励_傻大方

按关键词阅读：

在PyStan中应用贝叶斯回归
鼓励您在参与本文之前检查一下此概念性背景。
设定Stan [1]是用于贝叶斯模型拟合的计算引擎。它依赖于哈密顿量的蒙特卡罗（HMC）[2]的变体来从各种贝叶斯模型的后验分布中采样。
以下是设置Stan的详细安装步骤：
对于MacOS：
· 安装miniconda / anaconda
· 安装xcode
· 更新您的C编译器：conda install clang_osx-64 clangxx_osx-64 -c anaconda
· 创建一个环境stan或pystan
· 输入conda install numpy来安装numpy或将numpy替换为您需要安装的软件包
· 安装pystan：conda install -c conda-forge pystan
· 或者：pip install pystan
· 同时安装：arviz ， matplotlib ， pandas ， scipy ， seaborn ， statsmodels ， pickle ， scikit-learn ， nb_conda和nb_conda_kernels
设置完成后，我们可以打开（Jupyter）笔记本并开始我们的工作。首先，让我们使用以下内容导入库：
import pystanimport pickleimport numpy as npimport arviz as azimport pandas as pdimport seaborn as snsimport statsmodels.api as statmodimport matplotlib.pyplot as pltfrom IPython.display import Imagefrom IPython.core.display import HTML投币推理回想一下在《概念导论》中我谈到过如何在地面上找到一枚硬币并将其抛掷K次以检查它是否公平。
我们选择了以下模型：
一文看懂如何使用（Py）Stan进行贝叶斯推理文章插图
下面的概率质量函数对应于Y：
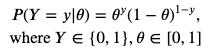文章插图
首先，通过使用NumPy的随机功能进行仿真，我们可以了解参数为a = b = 5的先验行为：
sns.distplot(np.random.beta(5,5, size=10000),kde=False)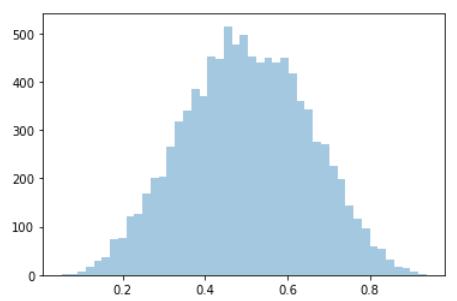 一文看懂如何使用（Py）Stan进行贝叶斯推理文章插图
如概念背景中所述，此先验似乎是合理的，因为其对称性约为0.5 ，但仍可能在任一方向上产生偏差。然后，我们可以使用以下语法在pystan中定义模型：
· 数据对应于我们模型的数据。在这种情况下，整数N对应于抛硬币的次数， y对应于长度为N的整数的向量，该向量将包含我的实验观察结果。
· 参数对应于我们模型的参数，在这种情况下为theta或获得"头部"的概率。
· 模型对应于我们的先验（β）和可能性（bernoulli）的定义。
# bernoulli modelmodel_code = """data {int N;int y[N];}parameters {real theta;}model {theta ~ beta(5, 5);for (n in 1:N)y[n] ~ bernoulli(theta);}"""data = http://kandian.youth.cn/index/dict(N=4, y=[0, 0, 0, 0])model = pystan.StanModel(model_code=model_code)fit = model.sampling(data=data,iter=4000, chains=4, warmup=1000)la = fit.extract(permuted=True)# return a dictionary of arraysprint(fit.stansummary())请注意， model.sampling的默认参数是iter = 1000 ， chains = 4和warmup = 500 。我们会根据时间和可用的计算资源进行调整。
· iter≥0对应于我们的每条MCMC链的运行次数（对于大多数应用程序，其运行次数不得少于1,000）
· warmup或"burn-in"≥0对应于我们采样开始时的初始运行次数。考虑到这些链条在运行之初就非常不稳定和幼稚，实际上，我们通常将这个量定义为丢弃第一个B =warmup样本数，否则我们会在估计中引入不必要的噪声。
· chains≥0对应于我们样本中的MCMC链数。
以下是上述模型的输出：
· 我们θ的后均值约为0.36 <0.5 。尽管如此， 95％的后可信区间很宽：（0.14 ， 0.61）。因此，我们可以认为结果在统计上不是结论性的，但它指向偏见而没有跳到0 。
应用回归：每加仑汽车和英里数（MPG）一文看懂如何使用（Py）Stan进行贝叶斯推理文章插图
Image by Susan Sewert from Pixabay
让我们构建一个贝叶斯线性回归模型来解释和预测汽车数据集中的MPG 。尽管我的方法是传统的基于可能性的模型，但我们可以（并且应该！）使用原始ML训练检验分裂来评估我们的预测质量。
该数据集来自UCI ML存储库，包含以下信息：
我们为什么不坚持我们的基础知识并使用标准的线性回归？ [3]回顾其以下功能形式：
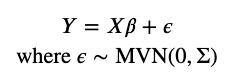一文看懂如何使用（Py）Stan进行贝叶斯推理文章插图
现在，对于贝叶斯公式：
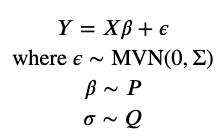文章插图
尽管前两行看起来完全一样，但是现在我们需要为β和σ（以及α ，为了表示简单起见，我选择将其吸收到β向量中）建立先验分布。