您可以在此处询问有关Σ的信息 。这是一个N（训练观察数）x P（系数/特征数）矩阵 。在标准线性回归情况下 ， 要求此Σ是对角矩阵 ， 且沿对角线有σ（观测值之间的独立性） 。
在执行EDA时 ， 您应该始终考虑以下几点：
· 我的可能性是多少？
· 我的模特应该是什么？ 互动与没有互动？ 多项式？
· 我的参数（和超参数）是什么？应该选择哪种先验条件？
· 我应该考虑任何聚类 ， 时间或空间依赖性吗？
EDA与任何类型的数据分析一样 ， 至关重要的是首先了解我们感兴趣的变量/功能以及它们之间的相互关系 。
首先加载数据集：
cars_data = http://kandian.youth.cn/index/pd.read_csv("~/cars.csv").set_index("name")print(cars_data.shape)cars_data.head()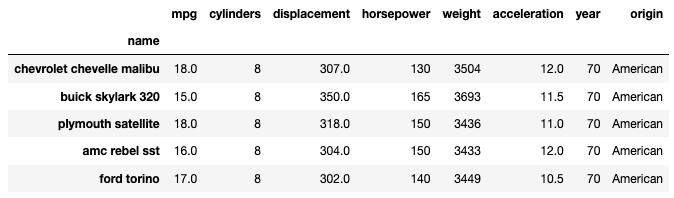文章插图
让我们检查一下目标变量和预测变量之间的关系（如果有）：
文章插图
There appears to be some interesting separation between American and Japanese cars w.r.t. mpg.
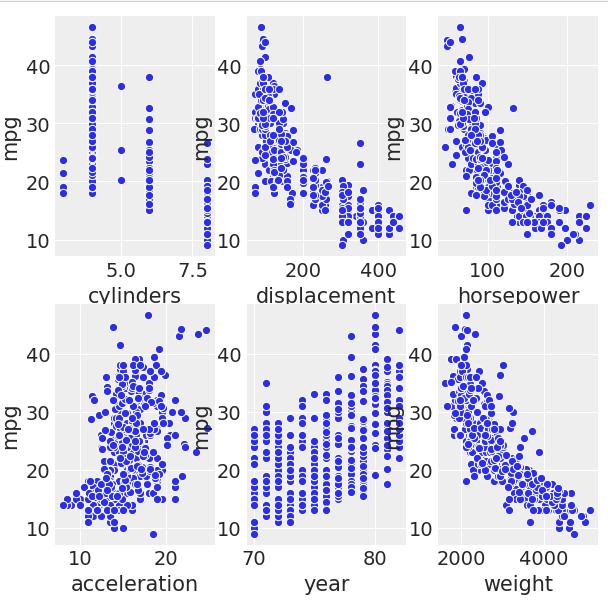
现在 ， 让我们检查一下数字变量和mpg之间的关系：
· 我更喜欢形象化这些关系而不是计算相关性 ， 因为它给了我关于它们之间关系的视觉和数学意义 ， 超越了简单的标量 。
文章插图
All but year and acceleration are negatively related to mpg, i.e., for an increase of 1 unit in displacement, there appears to be a decrease in mpg.
训练/拟合让我们准备数据集以进行拟合和测试：
from numpy import randomfrom sklearn import preprocessing, metrics, linear_modelfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import mean_squared_errorrandom.seed(12345)cars_data = http://kandian.youth.cn/index/cars_data.set_index('name')y = cars_data['mpg']X = cars_data.loc[:, cars_data.columns != 'mpg']X = X.loc[:, X.columns != 'name']X = pd.get_dummies(X, prefix_sep='_', drop_first=False) X = X.drop(columns=["origin_European"]) # This is our reference categoryX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=0)X_train.head()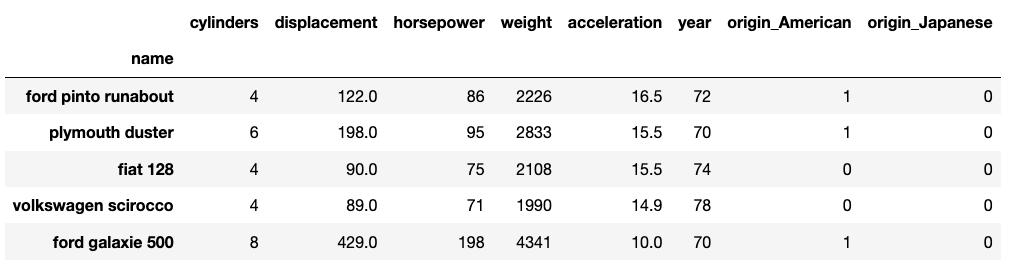文章插图
现在进入我们的模型规范 ， 它与上面的抛硬币问题没有实质性的区别 ， 除了我使用矩阵符号来尽可能简化模型表达式的事实之外：
# Succinct matrix notationcars_code = """data {int N; // number of training samplesint K; // number of predictors - 1 (intercept)matrix[N, K] x; // matrix of predictorsvector[N] y_obs; // observed/training mpgint N_new;matrix[N_new, K] x_new;}parameters {real alpha;vector[K] beta;real sigma;vector[N_new] y_new;}transformed parameters {vector[N] theta;theta = alpha + x * beta;}model {sigma ~ exponential(1);alpha ~ normal(0, 6);beta ~ multi_normal(rep_vector(0, K), diag_matrix(rep_vector(1, K)));y_obs ~ normal(theta, sigma);y_new ~ normal(alpha + x_new * beta, sigma); // prediction model}"""· 数据与我们模型的数据相对应 ， 如上面的抛硬币示例所示 。
· 参数对应于我们模型的参数 。
· 此处经过转换的参数使我可以将theta定义为模型在训练集上的拟合值
· 模型对应于我们对sigma ， alpha和beta的先验定义 ， 以及我们对P（Y | X ， α ， β ， σ）的似然性（正常）的定义 。
在对初始数据进行检查之后 ， 选择了以上先验条件：
· 为什么在σ上有指数先验？ 好吧 ， σ≥0（根据定义） 。为什么不穿制服或伽玛呢？ PC框架[4]-我的目标是最简约的模型 。
· 那么α和β呢？ 在正常情况下 ， 最简单的方法是为这些参数选择常规先验 。
· 为什么要对β使用multi_normal（）？ 数学统计中有一个众所周知的结果 ， 该结果表明 ， 长度为<∞且具有单位对角协方差矩阵且向量均值μ<∞的多重正态随机变量（向量W）等效于以下独立独立正态随机变量w的向量 N（μ ， 1）分布 。
stan的有趣之处在于 ， 我们可以要求在测试集上进行预测而无需重新拟合-而是可以在第一个调用中从stan请求它们 。
· 我们通过在上面的单元格中定义t_new来实现这一点 。
· theta是我们对训练集的合适预测 。
我们指定要提取的数据集 ， 并继续从模型中取样 ， 同时将其保存以备将来参考：
cars_dat = {'N': X_train.shape[0],'N_new': X_test.shape[0],'K': X_train.shape[1],'y_obs': y_train.values.tolist(),'x': np.array(X_train),'x_new': np.array(X_test)}sm = pystan.StanModel(model_code=cars_code)fit = sm.sampling(data=http://kandian.youth.cn/index/cars_dat, iter=6000, chains=8)# Save fitted model!with open('bayes-cars.pkl', 'wb') as f:pickle.dump(sm, f, protocol=pickle.HIGHEST_PROTOCOL)# Extract and print the output of our modella = fit.extract(permuted=True)print(fit.stansummary())