选自Medium
作者：Rahul Agarwal
机器之心编译
参与：高璇、杜伟
作为数据科学家 ， 我们已经对 Pandas 或 SQL 等关系数据库非常熟悉了 。 我们习惯于将用户属性以列的形式展示在行中 。 但现实世界的数据果真如此吗？
在互联世界中 ， 用户不能被视为独立的实体 。 他们之间存在一定的关系 ， 我们有时希望在构建机器学习模型时考虑到这些关系 。
在关系数据库中 ， 我们无法在不同的行（用户）之间利用这种关系 ， 但在图数据库中 ， 这样做非常简单 。
在这篇文章中 ， 我们将讨论一些数据科学家应该了解的非常重要的图算法 ， 以及如何使用 Python 实现它们 。
连接组件
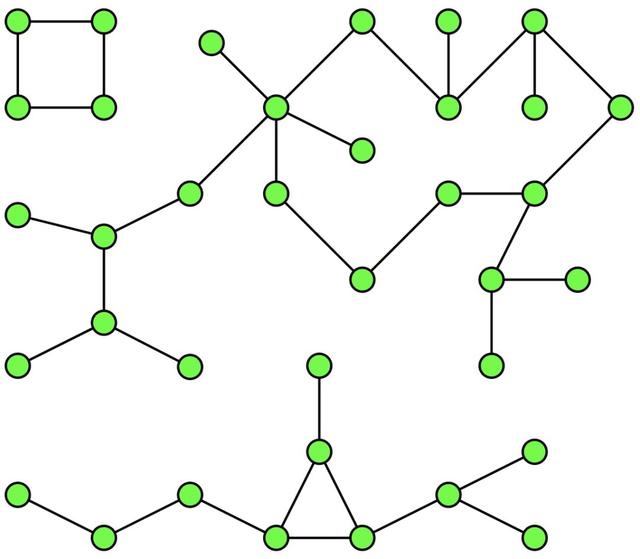文章插图
我们都知道聚类的工作机制 ， 你可以将连接组件视为一种在关联/连接数据中查找集群/个体的硬聚类算法 。
举个例子：假设你有连接世界上任何两个城市道路的数据 。 现在你需要找出世界上所有大洲以及它们所包含的城市 。
你将如何实现这一目标呢？
我们采用的连接组件算法是基于广度优先搜索算法（Breadth First Search ， BFS）/深度优先搜索算法（Depth First Search ， DFS）的特殊情况 。 这里不再展开介绍工作原理 ， 我们只看一下如何使用 Networkx 启动和运行此代码 。
应用
从零售角度看：假设我们有很多客户使用大量账户 。 使用连接组件算法的一种方法是在这个数据集中找出不同的族 。
我们可以根据相同的信用卡使用情况、相同地址、相同手机号码来建立某些客户 ID 之间的连接 。 一旦有这些连接 ， 我们就可以运行连接组件算法为有连接的客户创建单个集群 ， 然后为其分配一个家庭 ID 。
然后 ， 我们可以利用这些家庭 ID ， 根据家庭需求提供个性化推荐 。 我们还可以利用家庭 ID ， 通过创建基于家庭的分组功能来推进分类算法 。
从金融角度：另一个用例是利用这些家庭 ID 抓捕诈骗犯 。 如果某个帐户有过被欺诈经历 ， 那么关联帐户很容易再次受到欺诈 。
实施的可能性仅仅受到自身想象力的限制 。 （想象力越丰富 ， 算法的应用越广泛 。 ）
代码
我们将使用 Python 中的 Networkx 模块来创建和分析图 。 下面以包含城市和城市间距离信息的图为例 ， 实现我们的目的 。
文章插图
带有随机距离的图
首先创建一个带有城市名（边）和距离信息的列表 ， 距离代表边的权重 。
edgelist = [['Mannheim', 'Frankfurt', 85], ['Mannheim', 'Karlsruhe', 80], ['Erfurt', 'Wurzburg', 186], ['Munchen', 'Numberg', 167], ['Munchen', 'Augsburg', 84], ['Munchen', 'Kassel', 502], ['Numberg', 'Stuttgart', 183], ['Numberg', 'Wurzburg', 103], ['Numberg', 'Munchen', 167], ['Stuttgart', 'Numberg', 183], ['Augsburg', 'Munchen', 84], ['Augsburg', 'Karlsruhe', 250], ['Kassel', 'Munchen', 502], ['Kassel', 'Frankfurt', 173], ['Frankfurt', 'Mannheim', 85], ['Frankfurt', 'Wurzburg', 217], ['Frankfurt', 'Kassel', 173], ['Wurzburg', 'Numberg', 103], ['Wurzburg', 'Erfurt', 186], ['Wurzburg', 'Frankfurt', 217], ['Karlsruhe', 'Mannheim', 80], ['Karlsruhe', 'Augsburg', 250],["Mumbai", "Delhi",400],["Delhi", "Kolkata",500],["Kolkata", "Bangalore",600],["TX", "NY",1200],["ALB", "NY",800]]让我们使用 Networkx 创建一个图:
g = nx.Graph()for edge in edgelist: g.add_edge(edge[0],edge[1], weight = edge[2])现在我们想从这张图中找出不同的大洲及其城市 ， 这可以使用连接组件算法来实现：
for i, x in enumerate(nx.connected_components(g)): print("cc"+str(i)+":",x)------------------------------------------------------------cc0: {'Frankfurt', 'Kassel', 'Munchen', 'Numberg', 'Erfurt', 'Stuttgart', 'Karlsruhe', 'Wurzburg', 'Mannheim', 'Augsburg'}cc1: {'Kolkata', 'Bangalore', 'Mumbai', 'Delhi'}cc2: {'ALB', 'NY', 'TX'}如你所见 ， 只需要利用顶点和边 ， 我们就能够在数据中找到不同的组件 。 该算法可以在不同的数据上运行 ， 从而满足上面提到的各种用例 。
最短路径
继续使用上述示例 ， 现在我们有德国城市及城市之间距离的图 。 如何找到从法兰克福（起始节点）到慕尼黑的最短距离？我们用来解决此问题的算法被称为 Dijkstra 。 用 Dijkstra 自己的话说：
从鹿特丹到格罗宁根旅行的最短路线是什么？这就是最短路径算法 ， 我花了大约 20 分钟设计了它 。 一天早上 ， 我和我的未婚妻在阿姆斯特丹购物 ， 累了 ， 我们便坐在咖啡馆的露台上喝咖啡 ， 我只想着能否实现最短路径算法 ， 然后我成功了 。

稿源：(未知)

【傻大方】网址：http://www.shadafang.com/c/111J2H962020.html

标题：算法|PageRank、最小生成树：ML开发者应该了解的五种图算法