按关键词阅读: 算法 Kassel Frankfurt Augsburg Mannheim
正如我所说 , 这是一个二十分钟的发明 。 事实上 , 它发表于 1959 年 , 现在来看它的可读性也非常高 。 它之所以如此美妙 , 其中一个原因就是我没用笔纸就设计了它 。 后来我才知道 , 没有笔纸设计的有点之一是你不得不避免所有可避免的复杂问题 。 最终 , 令我惊讶的是 , 这个算法成为我的著名成果之一 。
应用
Dijkstra 算法的变体在 Google 地图中有着广泛使用 , 用于寻找最短路线 。
假设你有沃尔玛商店中各个过道位置和过道之间距离的数据 。 您希望为从 A 到 D 的顾客提供最短路径 。
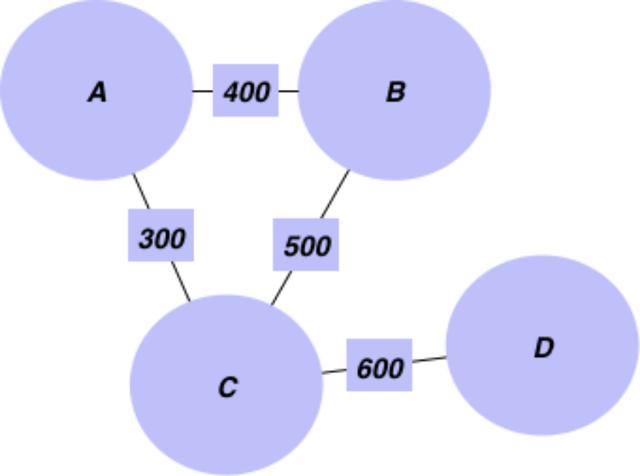 文章插图
文章插图
你已经看到 LinkedIn 显示一级连接和二级连接的方式 。 而这背后的机制是什么呢?
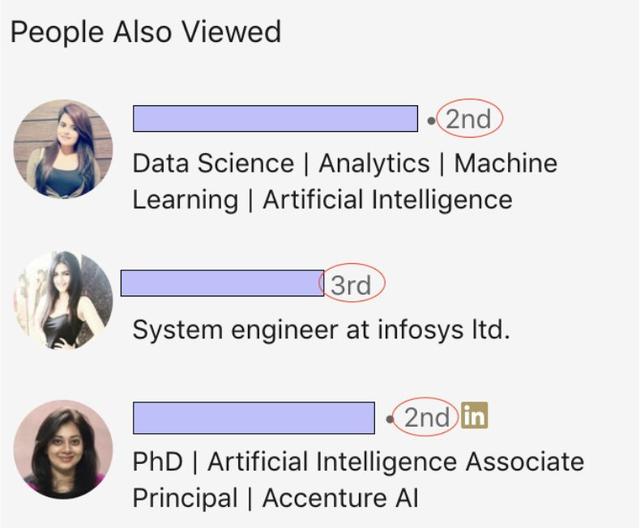 文章插图
文章插图
代码
print(nx.shortest_path(g, 'Stuttgart','Frankfurt',weight='weight'))print(nx.shortest_path_length(g, 'Stuttgart','Frankfurt',weight='weight'))--------------------------------------------------------['Stuttgart', 'Numberg', 'Wurzburg', 'Frankfurt']503你也可以找到所有对之间的最短路径:
for x in nx.all_pairs_dijkstra_path(g,weight='weight'): print(x)--------------------------------------------------------('Mannheim', {'Mannheim': ['Mannheim'], 'Frankfurt': ['Mannheim', 'Frankfurt'], 'Karlsruhe': ['Mannheim', 'Karlsruhe'], 'Augsburg': ['Mannheim', 'Karlsruhe', 'Augsburg'], 'Kassel': ['Mannheim', 'Frankfurt', 'Kassel'], 'Wurzburg': ['Mannheim', 'Frankfurt', 'Wurzburg'], 'Munchen': ['Mannheim', 'Karlsruhe', 'Augsburg', 'Munchen'], 'Erfurt': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Erfurt'], 'Numberg': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg'], 'Stuttgart': ['Mannheim', 'Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})('Frankfurt', {'Frankfurt': ['Frankfurt'], 'Mannheim': ['Frankfurt', 'Mannheim'], 'Kassel': ['Frankfurt', 'Kassel'], 'Wurzburg': ['Frankfurt', 'Wurzburg'], 'Karlsruhe': ['Frankfurt', 'Mannheim', 'Karlsruhe'], 'Augsburg': ['Frankfurt', 'Mannheim', 'Karlsruhe', 'Augsburg'], 'Munchen': ['Frankfurt', 'Wurzburg', 'Numberg', 'Munchen'], 'Erfurt': ['Frankfurt', 'Wurzburg', 'Erfurt'], 'Numberg': ['Frankfurt', 'Wurzburg', 'Numberg'], 'Stuttgart': ['Frankfurt', 'Wurzburg', 'Numberg', 'Stuttgart']})....最小生成树(Minimum Spanning Tree , MST)
现在我们面临另一个问题 。 假设我们在水管铺设公司或电线公司工作 。 我们需要使用最少的电线/管道来连接图中所有城市 。 我们如何做到这一点?
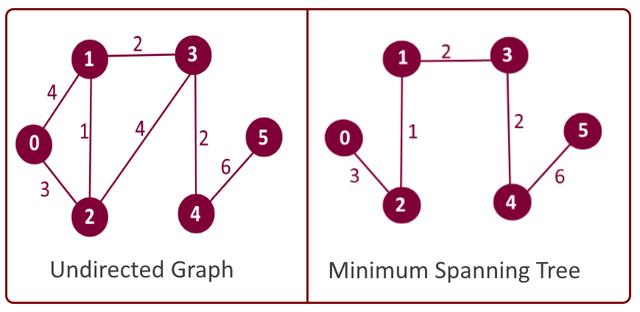 文章插图
文章插图
左:无向图;右:对应 MST
应用
- 最小生成树在网络设计中有直接应用 , 包括计算机网络、电信网络、交通网络、供水网络和电网(最初是为它们发明的) 。
- MST 用于近似旅行商问题 。
- 聚类:首先构建 MST , 然后使用类间距离和类内距离确定阈值 , 用于打破 MST 中某些边 。
- 图像分割:首先在图上构建 MST , 其中像素是节点 , 像素之间的距离基于某种相似性度量(颜色、强度等)
# nx.minimum_spanning_tree(g) returns a instance of type graphnx.draw_networkx(*nx.minimum_spanning_tree*(g))
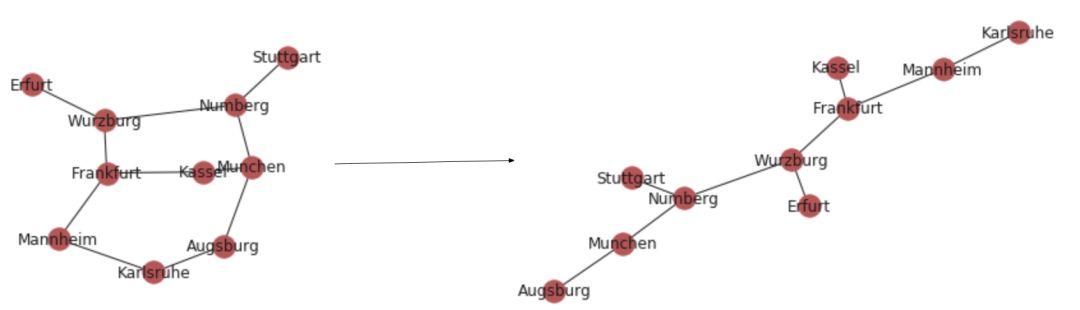 文章插图
文章插图左:无向图;右:对应 MST.
Pagerank
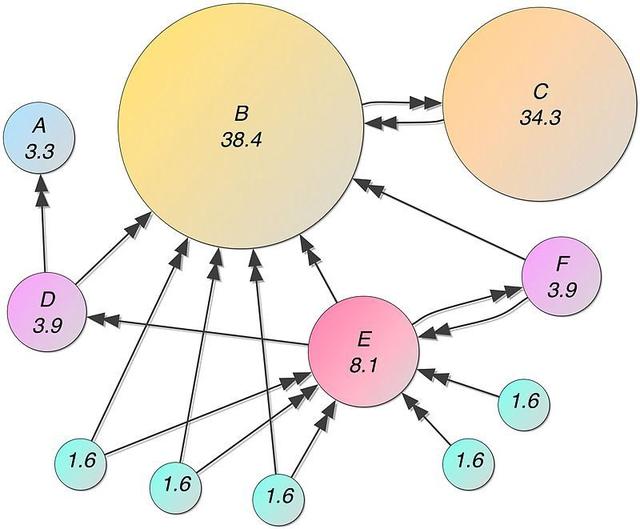 文章插图
文章插图上图为谷歌提供长期支持的页面排序算法(page sorting algorithm) 。 它根据输入和输出链接的数量和质量为页面打分 。
应用
Pagerank 可用于任何我们想要估算网络节点重要性的地方 。
- 它已被用于查找影响力最高的论文;
- 它已被 Google 用于网页排名;
- 它可用于将推文-用户和推文排序为节点 。 如果用户 A 跟帖用户 B , 则在用户之间创建链接;如果用户发推/转推 , 则在用户和推文之间建立链接;
- 推荐引擎 。
在本次练习中 , 我们将使用 Facebook 数据 。 我们在 facebook 用户之间有一个边/链接文件 。 首先通过以下方法创建 Facebook 图:
# reading the datasetfb = nx.read_edgelist('../input/facebook-combined.txt', create_using = nx.Graph(), nodetype = int)它是这样的:
pos = nx.spring_layout(fb)import warningswarnings.filterwarnings('ignore')plt.style.use('fivethirtyeight')plt.rcParams['figure.figsize'] = (20, 15)plt.axis('off')nx.draw_networkx(fb, pos, with_labels = False, node_size = 35)plt.show()
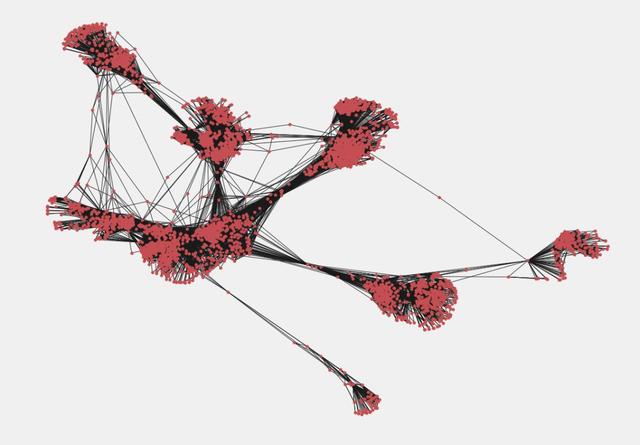 文章插图
文章插图Facebook 用户图

稿源:(未知)
【傻大方】网址:http://www.shadafang.com/c/111J2H962020.html
标题:算法|PageRank、最小生成树:ML开发者应该了解的五种图算法( 二 )