阿里华为等大厂如何处理数值精度/舍入/溢出问题 1

1 计算器的灾难:10%+10%到底等于几？

我们人类以为是 0.2 ，可是打开手机计算器试试呢？

解密国外计算程序使用的单步计算法。于是， a+b%表示a*(1+b%) 。所以，手机计算器实际上在计算10%*（1+10%）= 0.11 。
再通俗点一句话说清运算原理。以8+10%为例，为什么=8.8而不是8.1？一起读：8元钱，加上10%的小费，一共是8.8元。
最早的电子计算器并没有% ，是后来加的。作为后续改进，它一定解决了计算场景中的常用痛点，而绝不是脑残。我推测很可能是西方人计算折扣、小费、利息等常见场景。
2 满目疮痍的Double

浮点数四则运算
结果

由于计算机内部是以二进制存储数值的，浮点数亦是。 Java采用IEEE 754标准实现浮点数的表达和运算。比如， 0.1的二进制表示为0.0 0011 0011 0011… （0011 无限循环) ，再转换为十进制就是0.1000000000000000055511151231257827021181583404541015625 。计算机无法精确表示0.1 ，所以浮点数计算造成精度损失。
你可能觉得像0.1 ，其十进制和二进制间转换后相差很小，不会对计算产生什么严重影响。但积土成山，大量使用double作大量金钱计算，最终损失精度就是大量资金出入了。
一位“黑客”利用银行漏洞从PayPal、Google Checkout和其它在线支付公司窃取了5万多美元，每次只偷几美分。他所利用的漏洞是：银行在开户后一般会向帐号发送小额钱去验证帐户是否有效，数额一般在几美分到几美元左右。 Google Checkout和Paypal也使用相同的方法去检验与在线帐号捆绑的信用卡和借记卡帐号。用一个自动脚本开了58,000个帐号，收集了数以千计的超小额费用，汇入到几个个人银行账户中去。从Google Checkout服务骗到了$8,000以上的现金。银行注意到了这种奇怪的现金流动，和他取得联系， Largent解释他仔细阅读过相关服务条款，相信自己没做错事，声称需要钱去偿还债务。但Largent使用了假名，包括卡通人物的名字，假的地址和社会保障号码，因此了违反了邮件、银行和电信欺骗法律。别在中国尝试，这要判无期徒刑。
3 救世的BigDecimal我们知道BigDecimal ，在浮点数精确表达和运算的场景，一定要使用。不过，在使用BigDecimal时有几个坑需要避开。

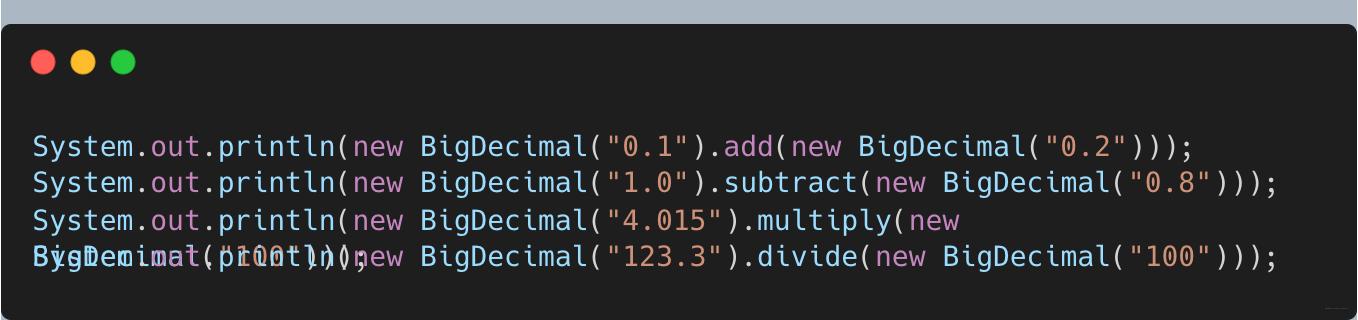
BigDecimal之前的四则运算
输出运算结果还是不精确，只不过是精度高了。

3.1 BigDecimal表示/计算浮点数且使用字符串构造器

文章插图

完美输出

无法调用BigDecimal传入Double的构造器，但手头只有一个Double ，如何转换为精确表达的BigDecimal？

Double.toString把double转换为字符串可行吗？
输出401.5000 。与上面字符串初始化100和4.015相乘得到的结果401.500相比，这里为什么多了1个0？BigDecimal有scale 小数点右边的位数precision 精度，即有效数字的长度

new BigDecimal(Double.toString(100))得到的BigDecimal的scale=1、precision=4；而new BigDecimal(“100”)得到的BigDecimal的scale=0、precision=3 。
BigDecimal乘法操作，返回值的scale是两个数的scale相加。所以，初始化100的两种不同方式，导致最后结果的scale分别是4和3：

private static void testScale() {BigDecimal bigDecimal1 = new BigDecimal("100");BigDecimal bigDecimal2 = new BigDecimal(String.valueOf(100d));BigDecimal bigDecimal3 = new BigDecimal(String.valueOf(100));BigDecimal bigDecimal4 = BigDecimal.valueOf(100d);BigDecimal bigDecimal5 = new BigDecimal(Double.toString(100));print(bigDecimal1); //scale 0 precision 3 result 401.500print(bigDecimal2); //scale 1 precision 4 result 401.5000print(bigDecimal3); //scale 0 precision 3 result 401.500print(bigDecimal4); //scale 1 precision 4 result 401.5000print(bigDecimal5); //scale 1 precision 4 result 401.5000}private static void print(BigDecimal bigDecimal) {log.info("scale {} precision {} result {}", bigDecimal.scale(), bigDecimal.precision(), bigDecimal.multiply(new BigDecimal("4.015")));}

4 浮点数的舍入和格式化应考虑显式编码，通过格式化表达式或格式化工具
4.1 明确小数位数和舍入方式

通过String.format使用%.1f格式化double/float的3.35浮点数
结果3.4和3.3

精度问题和舍入方式共同导致：double/float的3.35实际存储表示
3.3500000000000000888178419700125232338905334472656253.349999904632568359375String.format采用四舍五入的方式进行舍入，取1位小数， double的3.350四舍五入为3.4 ，而float的3.349四舍五入为3.3 。
我们看一下Formatter类的相关源码，可以发现使用的舍入模式是HALF_UP（代码第11行）：