按关键词阅读:

文章插图
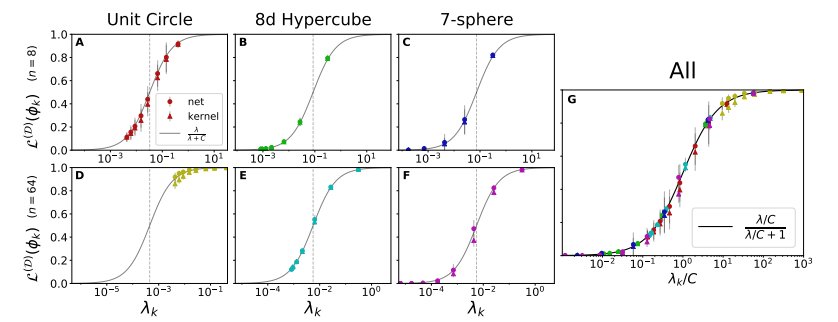
图 7:理论预测值与任意特征函数在多种输入空间上的真实的可学习性紧密匹配。每张图展示了关于训练集大小 n 的特征函数的可学习性。NTK 回归和通过梯度下降训练的有限宽度网络的理论曲线完美匹配。误差条反映了1由于数据集的随机选择造成的方差。(A)单位圆上正弦特征函数的可学习性。作者将单位圆离散化为 M=2^8 个输入点,训练集包含所有的输入点,可以完美地预测所有的函数。(B)8d 超立方体顶点的子集对等函数的可学习性。k值较高的特征函数拥有较小的特征值,其学习速率较慢。当 n =2^8 时,所有函数的预测结果都很完美。虚线表示 L-n/m 时的情况,所有函数的可学习性都与一个随机模型相关。(C)超球谐函数的可学习性。具有较高 k 的特征函数有较小的特征值,学习速率较慢,在连续的输入空间中,可学习性没有严格达到 1。
可学习性的统一形式
文章插图
文章插图
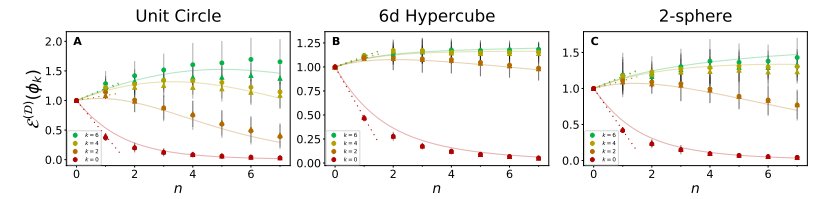
MSE会随着数据点被加入到较小的训练集中而增大。(A-C)在给定的 n 个训练点的 3 个不同域上分别学习 4 个不同特征模时,NTK 回归和有限网络的泛化 MSE。理论曲线与实验数据非常吻合。
宽度有限网络下的情况

文章插图
上图显式了 8d 超立方体上的四个特征模式的可学习性和训练集大小的关系,作者使用了一个包含 4 个隐藏层的网络进行学习,其网络宽度可变,激活函数为 ReLU。所有图表中的理论曲线都相同,虚线表示了朴素的、泛化性能极差的模型的可学习性。(A)严格的 NTK 回归下的可学习性(B-F)有限宽度网络的可学习性。随着宽度的减小,平均的可学习性微弱增大, 1σ误差增大。尽管如此,即使在宽度仅仅为 20 时,平均学习率也与理论预测值十分契合。
对此,一作回应道:没错,我们的理论假设知道完整的目标学习函数 f^,而在实践中我们只能看到一个训练集。
“但从折中的角度来使用该理论也是可行的。假设我们知道目标学习函数属于少数可能函数之一。 该理论原则上包含足够的信息来优化内核,因此它在所有可能函数上都具有很高的平均性能。 当然,目标学习函数永远不会只是少数几个离散选项中的一个。但是如果拥有一些关于目标学习函数的先验——例如,自然图像可能服从某些统计。另外,或许也可以从数据-数据内核矩阵中获得足够的信息来使用该理论,我们以后可能会探索这个方向!”

稿源:(雷锋网)
【傻大方】网址:http://www.shadafang.com/c/1115960cH021.html
标题:伯克利|UC伯克利发现「没有免费午餐定理」加强版:每个神经网络,都是一个高维向量( 四 )