按关键词阅读:
这样就可以计算f和f^之间的接近(可学习)程度。
作者还推导出了学习到的函数的所有一阶和二阶统计量的表达式,包括恢复之前的 MSE 表达式。如图 3 所示,这些表达式不仅对于核回归是相当准确的,而且也可以精准预测有限宽度的网络。
文章插图
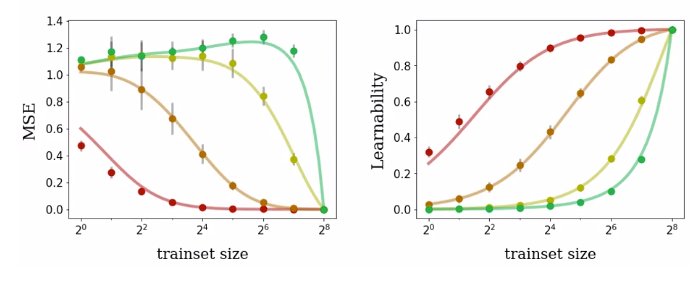
图 3:为四种训练集大小不同的布尔函数训练神经网络的泛化性能度量。无论是对 MSE 还是可学习性而言,理论预测结果(曲线)与真实性能(点)都能够很好地匹配。
文章插图
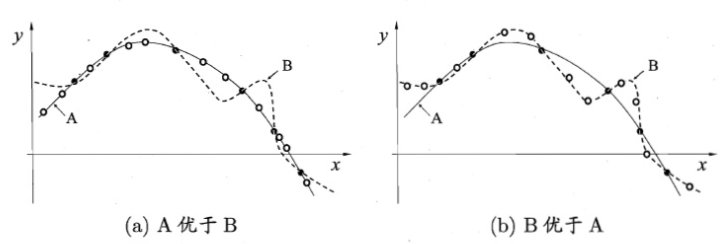
图 4:经典的没有免费午餐定理(来源:《机器学习》,周志华)
简单地说,如果某种学习算法在某些方面比另一种学习算法更优,则肯定会在其它某些方面弱于另一种学习算法。具体而言,没有免费午餐定理表明:
- 1)对所有可能的的目标函数求平均,得到的所有学习算法的「非训练集误差」的期望值相同;
- 2)对任意固定的训练集,对所有的目标函数求平均,得到的所有学习算法的「非训练集误差」的期望值也相同;
- 3)对所有的先验知识求平均,得到的所有学习算法的「非训练集误差」的期望值也相同;
- 4)对任意固定的训练集,对所有的先验知识求平均,得到的所有学习算法的的「非训练集误差」的期望值也相同。
所有核特征函数的可学习性与训练集大小正相关。
文章插图
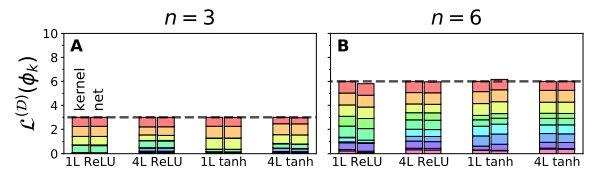
图 5:可学习性的特征函数之和始终为训练集的大小。
如图 5 所示,堆叠起来的柱状图显式了一个在十点域上的十个特征函数的随机 D 可学习性。堆叠起来的数据柱显示了十个特征函数的 D-可学习性,他们都来自相同的训练集 D,其中数据点个数为 3,我们将它们按照特征值的降序从上到下排列。每一组数据柱都代表了一种不同的网络架构。对于每个网络架构而言,每个数据柱的高度都近似等于 n。在图(A)中,对于每种学习情况而言,左侧的 NTK 回归的 D-可学习性之和恰好为 n,而右侧代表有限宽度网络的柱与左侧也十分接近。
神经核的谱分析结果

文章插图
图 6:神经核的谱分析使我们可以准确地预测学习和泛化的关键度量指标。
图 6 中的图表展示了带有四个隐藏层、激活函数为 ReLU 的网络学习函数的泛化性能,其中训练数据点的个数为 n。理论预测结果与实验结果完美契合。
- (A-F)经过完整 batch 的梯度下降训练后,模型学到的数据插值图。随着 n 增大,模型学到的函数越来越接近真实函数。本文提出的理论正确地预测出:k=2 时学习的速率比 k=7 时更快,这是因为 k=2 时的特征值更大。
- (G,J)为目标函数和学习函数之间的 MSE,它是关于 n 的函数。图中的点代表均值,误差条代表对称的 1σ方差。曲线展示出了两盒的一致性,它们正确地预测了 k=2 时 MSE 下降地更快。
- (H,K)为伪本征模的傅里叶系数,。由于 k=2 时的特征值更大,此时的傅里叶系数小于 k=7 时的情况。在这两种模式下,当被充分学习时,傅里叶系数都会趋向于 0。实验结果表明理论预测的 1与实验数据完美契合。

稿源:(雷锋网)
【傻大方】网址:http://www.shadafang.com/c/1115960cH021.html
标题:伯克利|UC伯克利发现「没有免费午餐定理」加强版:每个神经网络,都是一个高维向量( 三 )