不可区分混淆被实现，计算机科学家摘得这颗密码学皇冠上的明珠( 二 ) 机器之心报道编辑：魔王、小

文章插图
当时，很多人担心 iO 可能只是个无法实现的奇迹。
少即是多
2016 年， Huijia Lin 开始研究能否通过简单地减少多项式计算，来解决多重线性映射的缺陷。多重线性映射本质上是多项式计算的加密方式。 Jain 表示：「这些映射类似于多项式计算器，并与包含变量值的 secret locker 相连接。」机器接受用户输入的多项式，用户可以查看最终 locker ，以了解隐藏值能否使多项式的值为 0 。
为了确保该方案的安全性，用户不应了解有关其他 locker 的信息或者过程中生成的任何数字。 Sahai 表示：「我们希望这是真的，」但是，在研究人员提出的所有候选多重线性映射中，打开最终 locker 的过程中总是泄露出本该隐藏的计算信息。
文章插图
华盛顿大学副教授、该研究第二作者 Huijia Lin 。
研究人员提出的的多重线性映射均存在安全漏洞， Lin 想知道是否有一种方法，不必计算那么多不同种类的多项式也能构建 iO（因此更容易被安全地构建）。
四年前， Lin 发现了仅使用某些类型的多重线性映射构建 iO 的方法，这些映射计算「阶数（degree）」为 30 或者更小的多项式（这意味着每个项是最多 30 个变量的乘积）。接下来的几年中， Lin、Sahai 和其他研究者致力于如何将阶数降得更低。直到能够使用三阶多重线性映射构建 iO 。
理论上，这似乎是一个巨大的进步。但它仍存在一个问题：从安全的角度讲，三阶实际上与任意阶多项式处理机器一样差。
研究者了解如何安全构建的唯一多重线性映射是二阶或者更低阶的多项式处理机器。 Lin 与 Jain、Sahai 一道，试图找出用二阶多重线性映射构建 iO 的方法，他们在这个问题上挣扎了很久。
尽管探究过程充满艰辛，但最终他们提出了一种新的想法：由于 iO 需要三阶映射，而计算机科学家只能安全构建二阶映射，那么二者是否存在折中方案？比如 2.5 阶映射？
研究者设想了一个系统，其中某些 locker 具备清晰的窗口，因此用户能够查看其中包含的值。这使得机器不需要保护太多的隐藏信息。为了在高阶多重线性映射的能力与二阶映射的安全性之间取得平衡，机器可以使用高于二阶的多项式进行计算，但是有一个限制：隐藏变量的多项式必须为二阶。研究者称他们试图不隐藏太多信息，并证明能够安全构建这类混合 locker 系统。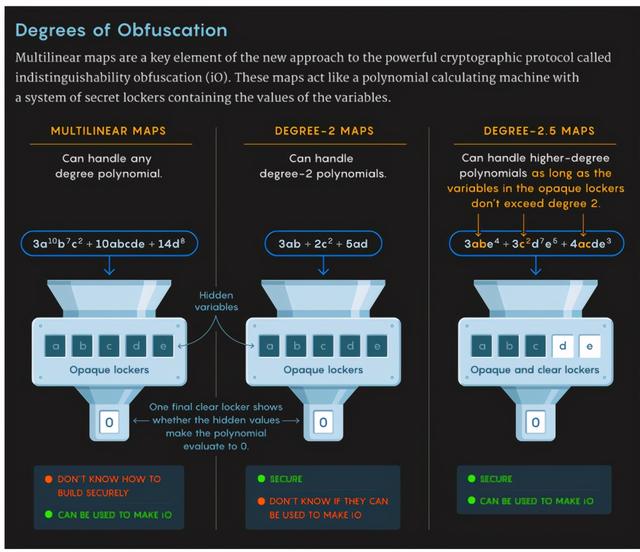
文章插图
要将这些功效较弱的多重线性映射转换为 iO ，还需要最后一个要素：一种新型的伪随机数生成器。它可以将一串随机位扩展为更长的字符串，并且仍具有随机性。
该研究的最终成果是能够避免多重线性映射安全弱点的 iO 协议。
该方案的安全性基于在在其他加密环境中被广泛使用的四个数学假设，这些假设历史悠久，研究时间最短的假设相关问题都可以追溯到 20 世纪 50 年代。
只可能有一种情况会打破该研究提出的新 iO 协议，那就是全功率量子计算机。四个假设之一易受量子攻击，但最近的一些研究已经提供了通往 iO 的另一种潜在途径，保证它即使受到量子攻击也是安全的，不过它所依赖的假设没有那么坚固。有研究者表示，在未来的研究中可以将两种方法结合起来，创造出既基于标准安全假设又能抵挡量子攻击的 iO 版本。
这可能会吸引新的研究人员加入。当理论上存在可行性时，那么就会有更多人愿意加入研究团队。毫无疑问，在该协议（或其变体）用于实际应用之前，计算机科学领域仍然有很多事要做。