|曼德尔球：分形几何最伟大的突破之一，视觉盛宴

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

在之前的文章中，我介绍了为了生成分形而迭代复数的历史和基础知识。从朱莉娅集合开始，我们通过定义和绘制曼德布罗特集合到达分形几何的心脏。
我们最初的好奇心确实得到了满足，就像数学中的许多发现一样，曼德尔布罗特集合的发现只会把我们带到一个新的问题领域，分形是否存在于不同的数系中？更具体地说，曼德尔布罗特集的三维对等物是什么？
序言【|曼德尔球：分形几何最伟大的突破之一，视觉盛宴】

鲁迪·洛克

一个叫鲁迪·洛克是一位杰出的数学家、计算机科学家和科幻小说作家，也是赛博朋克文化运动的创始人之一，他一直走在STEM世界的前沿（STEM是一门课程，其思想是通过跨学科和应用的方法对四个特定学科（科学，技术，工程和数学）的学生进行教育）。因此，在伯努瓦最初发表之后，他就敏锐地意识到了曼德尔布罗特集。富有创造力的洛克欣赏曼德尔布罗特集合，但是他的小说想象力将他推进到下一个步骤：存在一个数学上等价的曼德尔布罗特集合的3D结构。
不幸的是，洛克了解硬件的计算极限（80年代），知道所需的数十亿次计算可能是不可能的。受当时技术的限制，洛克做了他最擅长的事：他把它写下来。 1987年，洛克以一篇题为《如上所述，如下所述》的短篇小说首次以3D的形式写出了寻找圣杯（数学上等价的曼德尔布罗特集合的3D结构）的证据，这是理所当然的。在这篇小说中，他想象了曼德尔布罗特的发现，并将其命名为：曼德尔球。
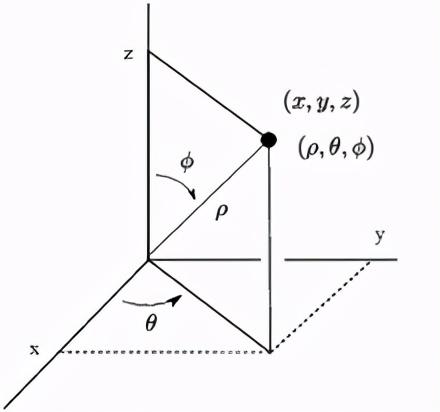
早期的尝试寻找三维等价物的关键在于数字系统中的不确定性。曼德尔布罗特集适合二维空间，因为复数有两个分量。我们能在三维空间中找到类似的数字系统吗？
数字系统问题
遍历的曼德尔布罗特公式（Z^2 + C）涉及两个操作：求和和复数的平方。创建一个可以进行加法运算的n元数组是很简单的，这就是线性代数中的向量空间。
但是，由于曼德尔布罗特公式还涉及到对数字进行平方，这需要在向量空间上使用乘法运算符（向量积），因此就产生了复杂性。具有向量乘积的向量空间称为域上的代数。为了了解为什么三维数字系统会有问题，让我们尝试创建一个。
我们从复数开始并引入第三个分量j 。接下来，我们需要保证复数和实数的某些性质也适用于我们的新数字系统；因为我们需要加法和乘法，所以我们特别关注保持结合律（a?（b+c）=（a?b）+（a?c））和交换律（a?b=b?a）不变。