克莱因瓶|最近,数学家通过四维空间几何解决了世纪性几何难题:环内的矩形

文章图片

文章图片
文章图片

文章图片
文章图片

文章图片

- 一个闭合环路包括所有矩形的角吗?
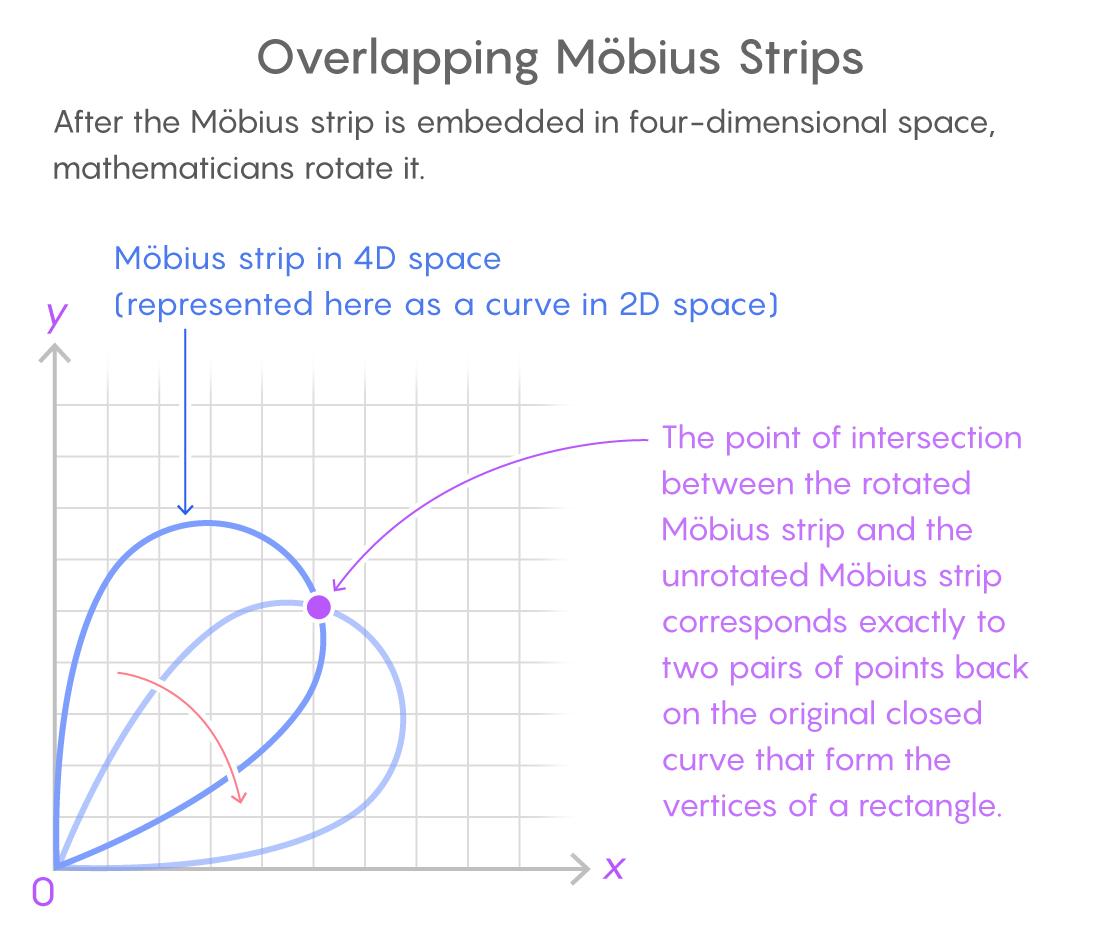
它以一个闭合的循环开始 。 格林和洛布研究的问题预测 , 基本上 , 每条这样的路径都包含四个点组成的集合 , 它们构成任意比例的矩形的顶点 。
虽然这个“矩形问题”看起来简单 , 但几十年来 , 数学家们一直在努力解决这个问题 。 当格林和洛布开始着手解决这个问题时 , 他们没有任何特别的理由认为自己会有所突破 。 在5月19日 , 当世界部分地区刚刚开始重新开放时 , 他们发布了一个解决方案 。
回顾矩形问题
矩形问题是德国数学家奥托·托普利兹在1911年提出的一个问题的一个近似分支 。 他预言 , 任何一条闭合曲线都包含四个可以连接起来形成正方形的点 。
要理解为什么这个问题如此困难 , 了解一些关于矩形问题所讨论的曲线类型是很重要的 , 这对格林和洛布的证明也很重要 。
这对搭档解决了一个关于既“连续”又“光滑”的闭合曲线的问题 。 光滑连续的曲线与仅仅连续但不光滑的曲线形成对比 。 有许多角的曲线的一个突出的例子是分形的科赫雪花 , 它实际上是由角组成的 。 科赫雪花和其他类似的曲线 , 无法用微积分和相关方法进行分析 , 这使得研究它们特别困难 。
一些连续的(非光滑的)曲线真的很糟糕 。
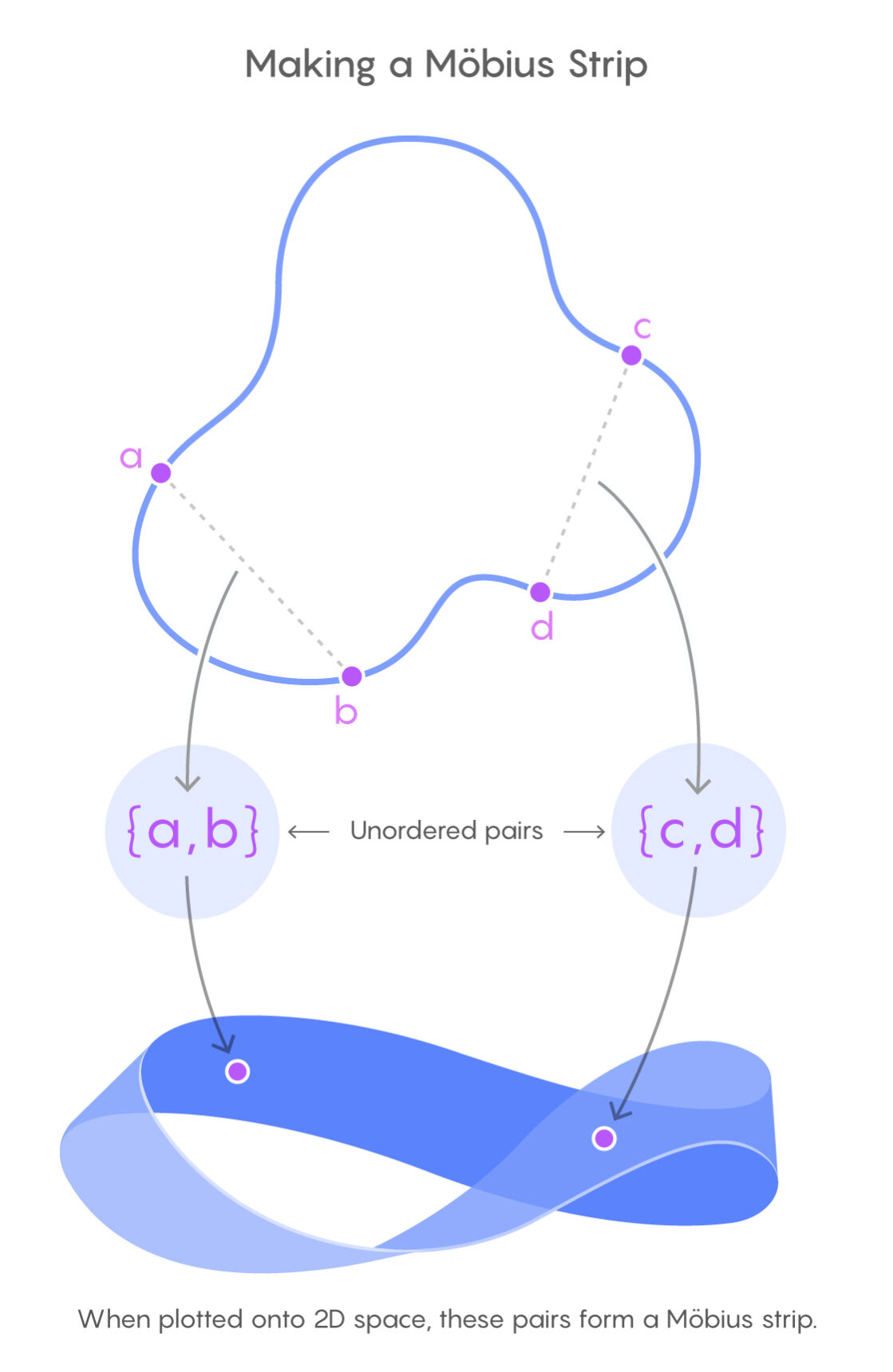
矩形桩问题的第一个重大进展是由赫伯特·沃恩在20世纪70年代末的一个证明中取得的 。 这个证明开创了一种思考矩形几何的新方法 。 沃恩没有把矩形看成四个连接点 , 而是把它看成两对彼此有特殊关系的点 。
画一个顶点标记为ABCD的矩形 , 从左上角顺时针方向 。 在这个矩形中 , 这对点AC(沿着矩形的对角线)之间的距离等于这对点BD(沿着另一条对角线)之间的距离 。 这两条线段也在它们的中点相交 。
因此 , 如果你在一个闭合的循环中寻找矩形 , 一个方法就是寻找它上面具有这一特性的对点:它们形成具有相同中点的等长线段 。 要找到它们 , 很重要的一点是要用一种系统的方式来思考它们 。
为了理解这是什么意思 , 让我们从一些更简单的东西开始 。 取标准数轴 , 在上面选择两个点上 , 比如7和8的 , 把它们画成xy平面上的一个点(7 , 8) , 像(7 , 7)这样的点也是允许的 。 现在考虑可以从数轴中提取的所有可能的数字对 。 如果你要画出所有这些点对 , 就填满了整个二维xy平面 。
- 手机丢失后不要慌,这几件事一定要做
- 共享充电宝越来越贵,已经惊动央视调查
- OpenAI推出数学推理证明模型,推理结果首次被数学家接受
- 微信昵称后面还能加根毛?朋友看到都懵了
- 手机欠费上征信,这个事非常不合理
- iPhone 13曝光,连王守义都看好的手机果然很“香”
- 联想手机走向衰败,网友为何说它一手好牌打稀烂
- 病毒|O泡果奶一份礼物有病毒么?O泡果奶一份礼物怎么关闭方法介绍
- “蚂蚁失足”,阿里一夜蒸发4500亿,赵薇尴尬了
- 为什么有人见不得中国5G建设快跑?
