量子力学|连续性方程—最实用的方程之一，它是如何体现守恒定律的？量子力学

文章图片

文章图片

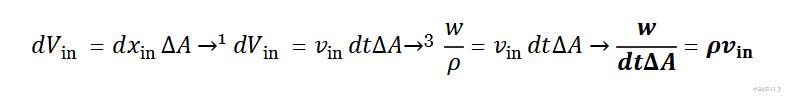
文章图片

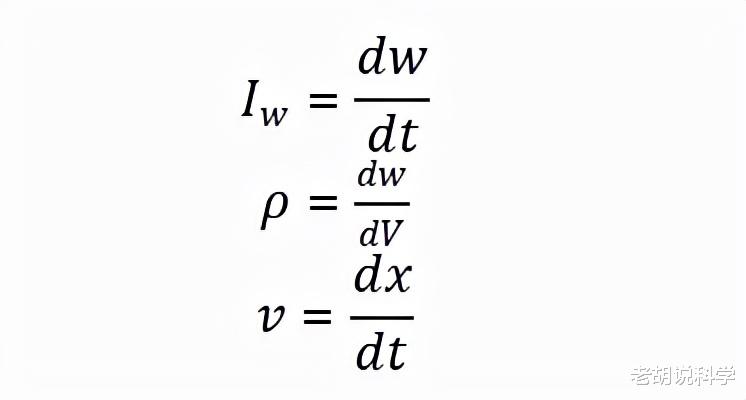
文章图片

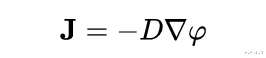
文章图片

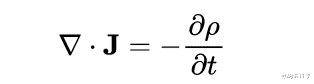
文章图片

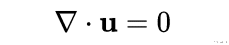
文章图片

连续性方程可以说是所有科学中应用最频繁的方程之一，几乎无处不在。从空气动力学和流体力学一直到电磁学和量子力学，这个方程主导了大多数的物理学领域。但是，这个方程究竟在直观层面上揭示了什么，为什么它如此重要？
简介?连续性方程是描述某种量w守恒传输的微分方程。
连续性方程的一般形式如下：
其中

ρ是单位体积内w量的数量，即其密度。
j是数量w的通量。
σ描述了w的产生（或移除）。

我们应该立即注意到的第一件事是，数量w没有被指定。因此，连续性方程本身并不是一个具体的方程，而是一种关于守恒量传输的方程的一般结构。
但在我们深入研究连续性方程的复杂性和应用之前，让我们退一步，建立必要的理论背景，以便更好地理解我们将要讨论的一切。
理论背景?强度性质（intensive property）和广度性质（extensive property）
我们可以把材料和系统的物理特性分为强度性质和广度性质
强度性质不取决于系统的大小或系统中材料的数量。强度性质的例子包括：

温度， T
密度， ρ
折射率， n
一个物体的硬度， η
沸点

相比之下，广度性质依赖于系统大小或系统中材料的数量。广度性质被认为是子系统的可加性。广度性质的例子包括：

质量， m
体积， V
长度， L
重量， w
熵

考虑到这些定义，我们可以给出连续性方程一个更普遍的定义。
例如，如果我们要处理的强度性质是质量密度，那么这个方程就是简单的质量守恒的表述：质量的变化是离开边界的东西和出现在边界内的东西的总和；没有任何质量是不被考虑的。
通量
在传输现象中，通量被定义为单位面积上一个量的流动速率。简单地说，通量就是在单位时间内，单位面积内流动的量。
在物理学中，有很多种类的通量。例如，我们将电通量定义为电场流经特定区域的速度。如果我们想用数学方法计算通量，我们必须采取表面积分，这也被称为通量积分。
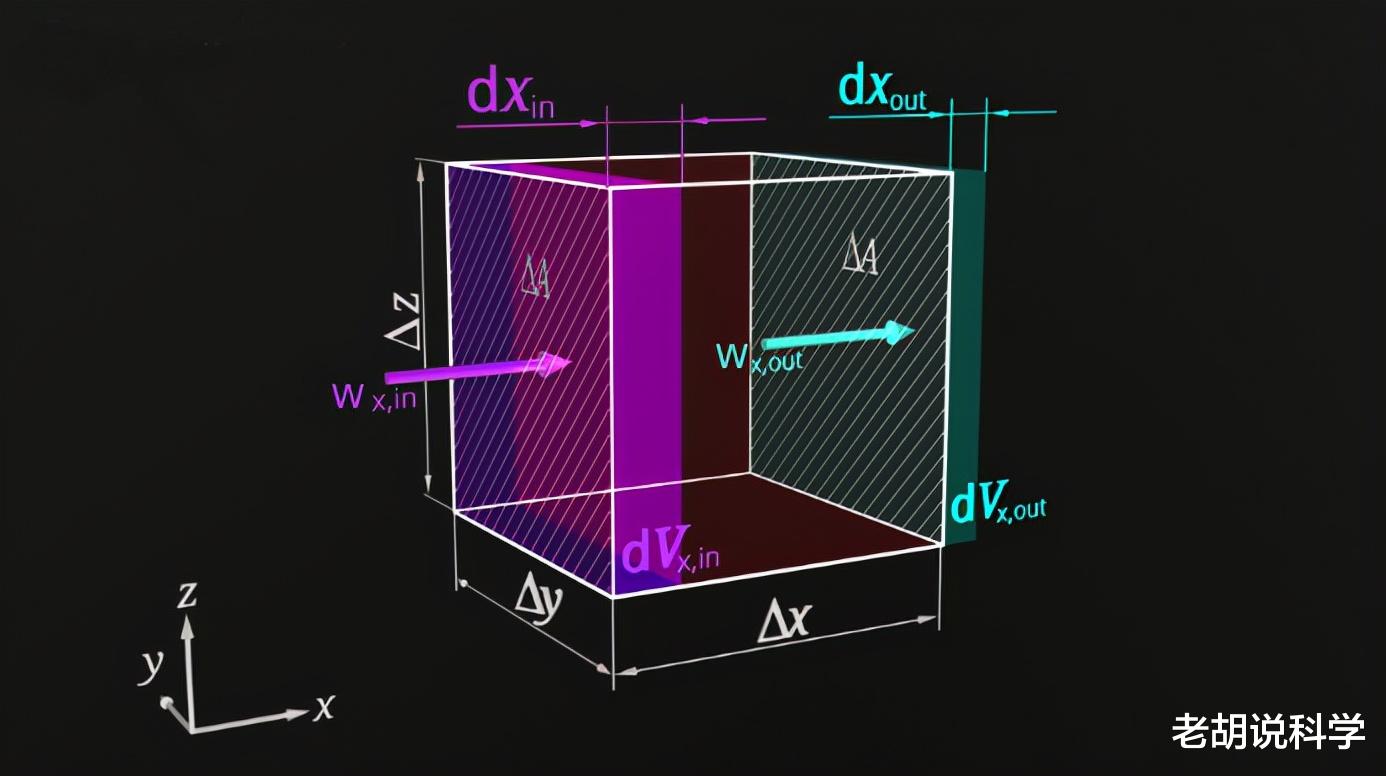
有一个重要的通量公式，在许多不同的情况下都会出现。假设有一个非常小的体积元素，其长度用Δx表示，其宽度用Δy表示，其高度用Δz表示。其所有的侧表面的面积为ΔA 。

体积元

我们知道，假设有一个量w——可以是质量、电荷等，正通过x方向流动，如上图所示。
在一个无限短的时间dt内，一个无限少的量dw_in ，流入体积，另一个无限少的的量dw_out ，正在离开体积。
现在，如果w以速度v_in进入体积元素，那么在时间dt内，它已经走过了一个无限小的距离dx_in 。因此，现在的无限小体积等于dx_in乘以ΔΑ 。最后，我们可以定义量w的体积密度， ρ 。下面是我们到目前为止所说的所有数学公式：
现在让我们做一些数学上的运算，以便得出一个通量的公式。
我们现在已经得出了一个一般的公式，因为还没有指定数量w具体是什么。
为了在数学上更加精确，我们可以取极限，当体积趋于0时， Δx ，Δy ，Δz ，ΔA分别变成dx dy dz da ，最终得到：
这里：
菲克定律?和扩散方程?首先，让我们回答一个基本问题。