爱因斯坦|推导爱因斯坦场方程，为广义相对论的度规创造一个“作用” 广义相对论|科学家

文章图片

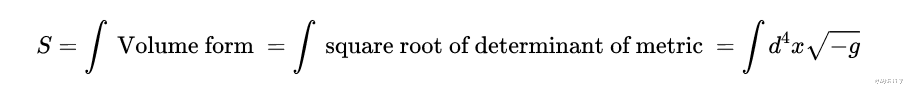
文章图片

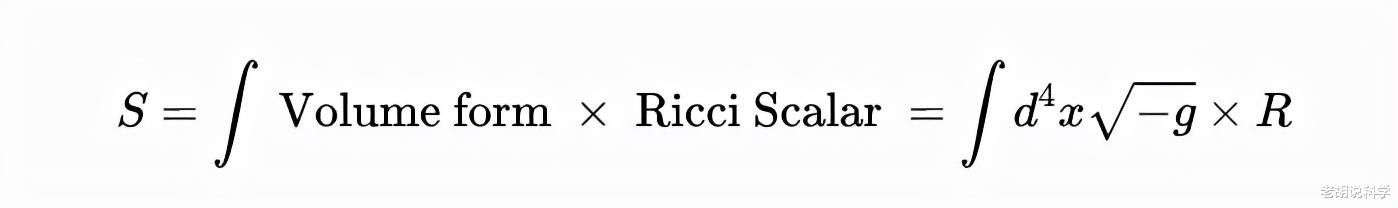
文章图片

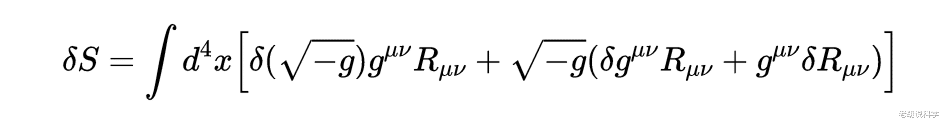
文章图片

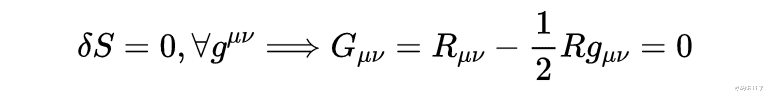
文章图片

在数学中，度规或距离函数是给出集合中每一对点元素之间的距离的函数。一个带有度规的集合称为度规空间。在微分几何中，度规的一个重要来源是度规张量。度规张量允许通过积分来确定沿着曲线的距离，从而确定度规。
在广义相对论中，时空是一个光滑的、坐标友好型（coordinate-friendly）的空间，称为流形（manifold）。度规g允许我们严格地定义这个流形中向量的距离和长度。我们把度规看成是一个矩阵，在流形上从点到点变化，解这个度规的方法是解爱因斯坦场方程。
那么问题来了，在广义相对论的框架内允许什么样的度规。一般来说，我们不可能写下任何我们想要的度规。那么，在自然界中哪些度规是被允许的？是否有一些方程式可以让我们确定一个度规的演变？
事实证明，物理上允许的度规是爱因斯坦场方程的解。爱因斯坦的场方程如下：
在右手边，符号T代表能量动量张量。能量动量张量编码了大质量物体（比如中子星）在时空中的能量。
左边包含了描述时空的关键属性。 R表示时空有多 \"弯曲\" 。左边的第一项是里奇曲率，它描述了宇宙的三维空间与平坦空间相比是如何弯曲的（弯曲程度）。它有两个希腊字母下标，因此它是一个2级张量（所以我们可以把它写成一个矩阵）。第二项描述了与平坦空间相比，体积是如何扭曲的。符号R被称为里奇标量。第三个项是宇宙学常数，带字母g的项是度规本身。
在这篇文章中，我想介绍一下这个方程是如何推导出的。
爱因斯坦-希尔伯特作用我们把度规当作一个动态的物理变量。首先通过在固定时间内对两点间的拉格朗日积分来构造一个作用；然后，为了找到经典粒子的路径，我们要找到使作用量最小的路径。
为了在广义相对论中做到这一点，我们将构建一个包含度规的作用。为了构建这个作用，必须想出一些合理的度规函数，然后测试所得到的运动方程是否与我们在经典情况下得到的一致。
一旦构建了一个作为度规函数的作用，我们就会尝试将这个作用最小化，以求得确切的度规是什么。由此得到的度规就是爱因斯坦场方程的解。将作用量最小化是一项技术上的挑战，但是我们只需要做一次计算。
构建爱因斯坦-希尔伯特作用?我们把从度规中构建的作用称为爱因斯坦-希尔伯特作用。我们唯一要处理的对象是度规g 。一个物体的 \"体积 \"完全取决于时空中的距离是如何定义的。我们可以用度规来定义时空中的体积概念（取其行列式的平方根）。度规的行列式的平方根是我们可以使用的一个自然的体积形式。这就给了我们一个提示，作用看起来应该像：
现在，我们唯一能做的就是把里奇标量提出来。里奇标量是一个实数，在流形中的每一点上都有一个值。当里奇标量在某一点为正时，如果有欧几里得度规，围绕该点的小球的体积比半径相同的小球的体积要小。如果里奇标量为负则相反。下面粉色的球是有度规g的球的体积，棕色球是用欧几里得平面度规感知的体积。
因此，构建作用的自然方式是把里奇标量放在体积形式的前面。这在下面的方程中显示。里奇标量用符号R来表示。
同样，里奇曲率张量也衡量空间的曲率与平坦空间的不同。
爱因斯坦-希尔伯特作用的极端?为了推导出爱因斯坦场方程，我们需要找到使作用量最小的度规。为了做到这一点，我们将对度规进行微小的扰动，看看作用S如何变化。我们希望作用S会发生微小的变化，我尝试写出一个表达式来说明作用发生了多大变化。
在数学上，我们把一个微小的变化称为 \"扰动\" 。因此，为了扰动度规，在度规上增加一个微小的项。这个微小的项是用希腊的delta符号表示的。我们对度规的扰动看起来像：