自动化|Martech 营销自动化从 AB 测试开始( 二 )
2. 流量正交实验每个独立实验为一层,一份流量穿越每层实验时,都会随机打散再重组,保证每层流量数量相同。
举个例子。假设现在有 2 个实验。
- 实验 A(实验组标记为 A1,对照组标记为 A2)分布于实验层 1,取用该层 100% 的流量;
- 实验 B(实验组标记为 B1,对照组标记为 B2)分布于实验层 2,也取用该层100% 的流量。
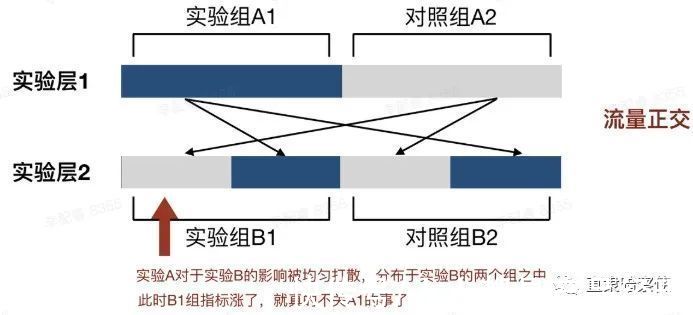
- 如果把 A1 组的流量分成 2 半,一份放进 B1 组,一份放进 B2 组;
- 再把 A2 组的流量也分成2半,一份放进 B1 组,一份放进 B2 组。
文章插图
【 自动化|Martech 营销自动化从 AB 测试开始】我们可以发现,因为 A1 组的一半流量在 B1 中,另一半流量在 B2 中,因此即使 A1 的策略会对实验 B 产生影响,那么这种影响也均匀的分布在了实验 B 的两个组之中;在这种情况下,如果 B1 组的指标上涨了,那么就可以排除 B1 是受 A1 影响才形成上涨。这就是流量正交存在的意义。
3. 互斥实验所有互斥实验使用同一流量层用户,但不共享用户,如果一个用户 / 设备命中了实验 A,就不会命中互斥的其他实验。
4. 实验指标在开始一个实验时,目的是对比对照组和实验组的某个或者某几个指标。如,分析活动页面主图的点击次数时,需要上报注册的点击事件,然后在 AB 测试中配置指标,即可看到实验中及实验后的指标对比。
5. 流量过滤对 AB 测试的目标用户增加一些限制条件,规定被实验命中的用户必须符合(或不符合)条件,比如针对某个用户分群,某些用户标签进行过滤,进而精准找到测试目标人群,这种限制条件即“流量过滤”。
6. 白名单用户在实验正式开启之前,通常需要先选择几名用户进入测试阶段,观察实验是否能够正常获取想要收集的数据,或执行流程是否符合预期。参与这一步的用户被称为“白名单用户”。
7. 置信区间置信度区间就是用来对一组实验数据的结果进行估计的区间范围。
举个例子,我们现在进行一个实验来体现活动落地页中的图案改变对用户购买率的影响,其中采用了新策略 B 的实验组,购买率提升均值为 5%,置信区间为[1.5%,8.5%]。
怎么理解此处的置信区间呢?由于在 AB 实验中我们采取小流量抽样的方式,样本不能完全代表总体,那么实际上策略 B 如果在总体流量中生效,不见得会获得 5% 的增长。
如果我们设策略 B 在总体流量中推行所导致的真实增长率为 μ,那么在这个案例中,μ 的真实取值会在 [1.5%,8.5%] 之间。
值得注意的是,μ 并不是 100% 概率落在这一区间里,在计算置信区间的过程中,我们会先取一个置信度,计算这一置信度下的置信区间是多少,AB 实验中我们通常计算 95% 置信度下的置信区间。
回到刚刚的例子,我们就可以得知,μ 的真实取值有 95% 的可能落在 [1.5%,8.5%] 之间。
8. 置信度在实际操作中,会遇到实验结论显示新策略有用,但实际上全量发布新策略后没用。
在统计学中称为第一类错误,用显著性水平 ( α ) 来描述实验者范这一类错误的概率,置信度 = 1 – α,当某个实验结论显著性指标 α < 5%,则置信度 > 95%,我们认为这个实验结论指标大概率是可信的,系统有超过 95% 的信心确认这个实验结论是准确的。
在 AB 测试中,由于只能抽取流量做小样本实验。样本流量的分布与总体流量不会完全一致,这就导致没有一个实验结果可以 100% 准确,即使数据涨了,也可能仅仅由抽样误差造成,跟我们采取策略无关。
在统计学中,置信度的存在就是为了描述实验结果的可信度。
9. 校验灵敏度 ( MDE )实际操作中,会遇到新策略其实有效,但实验没能检测出来。
在统计学中称为第二类错误,用 β 来描述实验者范这一类错误的概率,统计功效 = 1 – β,统计功效表示如果新策略是有效的,有多大概率在实验中能够检测出来。通常认为统计功效 > 80% 为有效检测 。
通过设置 MDE,并与新策略的目标提升率进行比较,来避免实验在灵敏度不足的情况下被过早做出非显著结论而结束,错失有潜力的新策略。MDE 越小,意味着要求测试的灵敏度越高,所需的样本量也越大。
- 庄俊|2022年小红书内容营销必看39条建议
- 自动化|移动办公效率太慢?硬盘盒搭配aigo固态硬盘,体验后真香
- 云安全|营销大王马斯克干的好事!0广告投入的特斯拉,市值突破万亿美元
- 洗衣机|2022年卤菜行业最主流的营销方式
- 心理学|营销的六大心理学效应(下)
- 冰雪运动|冰雪运动互联网平台营销影响力榜发布 | 数字品牌榜 x 氪体
- 社群|10天业绩150万+的社群营销攻略
- 网络营销|实时网络营销如何做?营销效果如何检测?
- b2b|一个“五脏六腑”俱全的B2B内容营销团队是怎样的?
- 自动化|为什么宁愿买荣耀手机,也不买小米手机?
