二叉状态树的结构,Part-1( 二 )
key和value , 两个数据都是字节数组(byte array) 。 RLP 理论上应该能帮助我们编码这两个数据吧?不那么见得 。 一棵十六进制树上的 key 是基于半字节(nibble-based)的 , 所以如果我们取出一个键的时候 , 它可能在半字节处就中止了 , 那问题就来了:我该怎么对齐数据呢?这里面必须要有一个设计抉择 。 结果是 , 我们使用一种叫做 “十六进制前缀(hex prefix)方法” 的函数来读取键数据 , 它会加入一个 header 来告诉我们所读的键的长度究竟是偶数个还是奇数个半字节 。
- 十六进制前缀编码方法使用第一个字节(即上文的 “头字节”)中的前半个字节来存储该键的长度(是奇数还偶数个半字节) 。 -
十六进制前缀方法还要求我们调整半字节的位置 。 举个例子 , 如果键的长度是奇数个半字节 , 那就把第一个半字节放到头字节的最后一个半字节的位置 。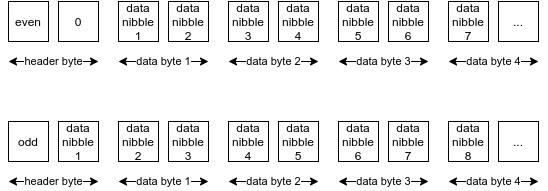 文章插图
文章插图
同样地 , 如果长度是奇数 , 但跟字节的终止位置对不齐(not byte-aligned) , 那么每一个半字节都必须位移 , 以使其能以少一个字节的长度来存储 。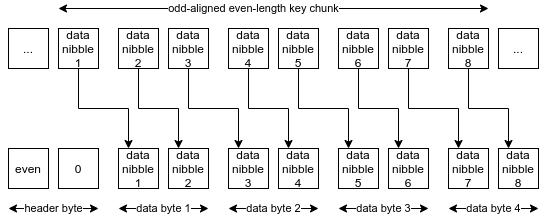 文章插图
文章插图
- 如果长度是偶数 , 但却是奇数对齐的(odd-aligned) , 那所有的半字节都要位移 4 个位 。 -所以 , 叶子节点最终是以RLP(HP(key_chunk), value)的形式来编码的 。
分支节点和太小的子节点一个分支节点(branch node)有 16 个子节点(childeren) , 每个字节点都占用半个字节 。 按照 RLP 的规则 , 分支节点只是一个其子节点哈希值的列表 , 也就是一个包含了 16 个字节数组的列表 。 如果某个子节点是空的 , 那就表示为一个空的数组(只是用一个独立的128来标注一个长度为 0 的数组) 。 世界上 , 列表中还有第 17 个条目 , 就是分支节点本身的值 , 但因为实践中都不使用它 , 所以列表的最后一个条目总是128 。 没错 , 正如你所料 , 这里又会产生很多麻烦 。 为了避免在数据库中为太小的对象创建条目 , 一个 RLP 编码值太小的节点就不会计算出哈希值 。 在这种情况下 , 其 RLP 编码会直接存储为一个原始数据的列表 , 而不是这个列表的哈希值 。 结果就是你在列表中鲜少找到数组开始的标记(128) , 反而常常找到另一个列表开始的标记(192) , 又给开发者出了很多难题 。 如果一个分支节点的 RLP 的数据总大小大于 32 , 那它就会被算成哈希值 。 大部分时候都是如此 , 因为 , 如果没有算成哈希值 , 那就意味着一个子节点的 RLP 数据大小已达最大值:16 个字节 。
延伸节点状态树上还有第三种节点 , 叫做延伸节点(extension node) , 我们放在下一篇文章中集中讨论 。 幸好 , 幸好 , 在 RLP 编码这一点上 , 它没有给我们增加任何麻烦 。
我们真的需要 RLP 吗?所有这些优化都是有用的吗?不见得呀 。
举个例子 , 假如我们不使用 rlp < 32 bytes这条规则 , 需要多占用多少存储空间呢?
跟今天全同步节点所需的约 300 GB 的存储空间相比 , 简直是微不足道 。
类似地 , 不使用十六进制前缀编码 , 也只会导致多占用 100 MB 的存储 , 也就是多占用 0.03% 。 只要仔细选择二进制 trie 的编码格式 , 这点差距就可以补回来 。
二进制 trie:送 RLP 入土为安在二级制 trie 上 , 分支节点会变得简单很多:一个节点最多只有两个子节点 , 可以由其哈希值来指出 。 一个 Keccak256/Sha256 的哈希值 , 也就是 32 个字节 。
在当前 , 显然的事情是 , 我们根本不需要一个能编码任意长度的值的通用编码方案 。 举个例子 , 假设新的二进制树种的每个节点都具有下列的字段:
- 左子节点哈希值 , 用作指针;
- 右子节点哈希值 , 用作指针;
- 值(可选) , 即存储在用于寻得此节点的键中(stored at the key used to get to this node)的值
- 前缀(可选) , 目的是替换十六进制 trie 中的延伸节点
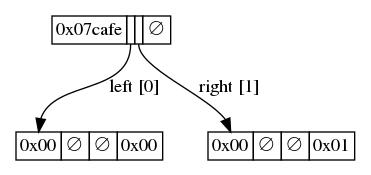 文章插图
文章插图- 例子中的树存储着键值对 (0xcafe, 0x00) 以及 (0xcaff, 0x01):根节点以键数据 “0xcafe” 和一个数字作为前缀;该数字表示最后一个字节中仅有 7 个比特用于存储前缀 。 然后该节点有两个指针指向其两个子节点 , 同时不包含值 。 每一个子节点都以空值为前缀(以 0x00 为标记) , 都有一个值 , 都没有子节点 。 -
- “树标提质”提升“软实力”数字经济时代创新载体大有可为
- 更改计算机待机睡眠状态时间方法,电脑设置关闭显示器时间教程
- 树莓派4安装Ubuntu20.04通过SD卡设置wifi
- 二叉树:搜索树的最小绝对差
- 二叉树:求搜索树中的众数
- pydotplus的安装、基本入门和决策树的可视化
- Clockwork推出定制套件 可将树莓派变身为便携式计算机
- 当手机状态栏显示“HD”,别不在意,你的话费可能偷偷在减少
- 二叉树:公共祖先问题
- 树欲静而风不止!中国光刻机迎来生机,ASML小动作不断
