深度模型压缩技术在智能座舱方案的探索与实践( 二 )
 文章插图
文章插图
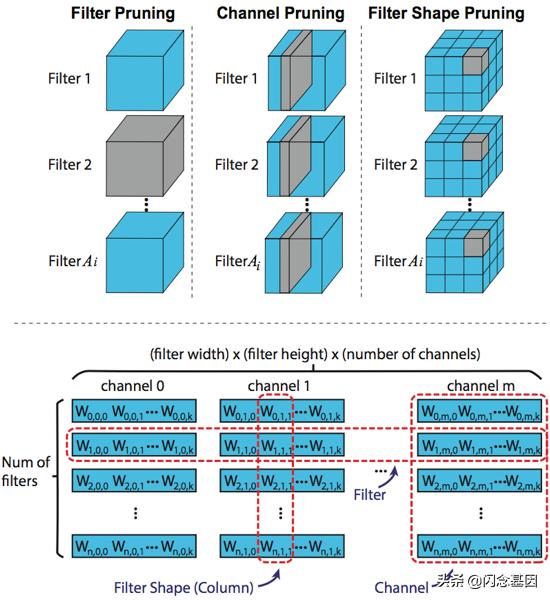
图3 不同的结构化剪枝策略: 基于卷积核的角度和通用矩阵乘算法(GEMM)的角度
在深度模型中 , 评价权重的重要程度的方式有多种 , 最常见的就是计算权重的绝对值(之和) , 即L1范数(L1 norm) , 通过该值的大小来判断是否重要 。 也有其他的方式 , 例如根据batch norm层的参数作为评估标准并进行卷积核剪枝等 。 很多模型剪枝算法都需要手工设计裁剪阈值或者比率 , 例如设置|w| < 0.01 , 或者设置每层的剪枝率 。 这种人为的设计过程需要依赖很多专业的经验 , 并且该过程需要反复尝试 。 因此人为设计剪枝的方案往往难以达到最优的效果并且浪费人工成本 。
2.1.1 自动化剪枝
如何解决这个问题呢?我们基于AutoML的思想 , 提出了自动结构化剪枝的算法框架AutoCompress , 能自动化的去寻找深度模型剪枝中的超参数 , 去除模型中不同层的参数冗余 , 替代人工设计的过程 , 从而满足嵌入式端上运行深度模型的实时性能需求 。
如图4所示 , 整个自动化通用流程主要可以分为四步 。 步骤一是行为抽样 , 步骤二是快速评估 , 步骤三是确定决策 , 步骤四是剪枝操作 。 由于超参数的搜索空间巨大 , 考虑到训练资源使用及时间成本 , 步骤一和步骤二需要快速进行 , 因此无法进行再训练(re-training)后去评估其效果 。 算法根据每层中量级最小的一部分权重直接进行剪枝评估 。 步骤三是根据搜索过程中产生的抽样和评估的集合对超参数进行决策 。 步骤四利用了动态正则的核心剪枝算法(ADMM , Alternating Direction Method of Multipliers)对模型进行结构化剪枝并生成结果 。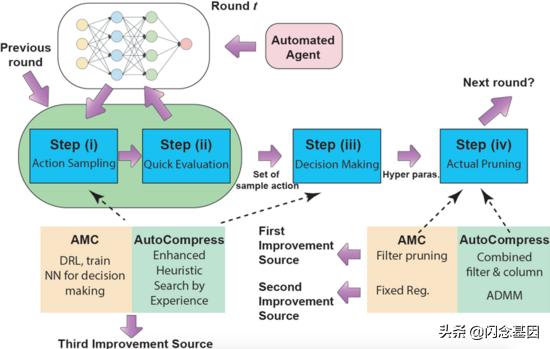 文章插图
文章插图
图4 自动化超参数决策框架的通用流程 , 以及性能提升来源
前三个步骤本质上是一个抽样-验证的搜索过程 , 因此 , 我们采用了启发式的模拟退火算法进行搜索 。 具体流程是 , 首先给定一个原始预训练大模型 , 我们会设置两种目标函数 , 根据权重数量或者根据运算数量(FLOPs , floating point operations) 。 整体搜索过程将进行若干轮 , 例如第一轮目标为压缩两倍权重数量 , 第二轮为四倍权重数量等 。 在每一轮搜索过程中 , 首先初始化一个动作(超参数) , 每次对动作进行一个扰动(超参数的小幅变化)生成新的动作 , 根据模拟退火算法原理 , 评估两个动作 , 如果新的动作评估结果好则接受 , 如果新的动作评估结果比原来差则以一定概率接受 。 每一轮算法中的温度T会下降 , 直到温度下降到某个阈值后停止搜索 。
2.1.2 ADMM剪枝算法
交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)是一种求解凸优化问题的非常强大的方法 。 在非凸优化问题 , ADMM虽然可能无法收敛到全局最优 , 但在很多应用中也表现的十分优异 。 这种方法的主要优势是:
- 将原问题的目标函数分解成若干可求解的子问题
- 子问题可以独立并高效的被求解
- 子问题可以迭代的求解
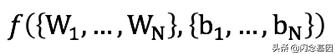 文章插图
文章插图其中W表示权重 , b表示bias 。 为了进行剪枝 , 在损失函数中对权重加入约束, e.g.,
加入约束后的损失函数由如下两部分组成 , 原始损失函数 和约束项的指示函数
 文章插图
文章插图, 公式如下:
 文章插图
文章插图上述优化问题的增广拉格朗日函数如下:
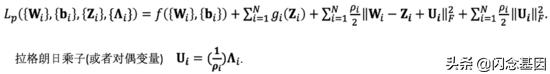 文章插图
文章插图通过ADMM , 将迭代地求解以下子问题实现深度模型稀疏化:
- 子问题(1):更新权重
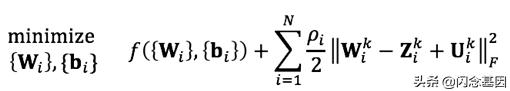 文章插图
文章插图- 子问题(2):更新正则化目标
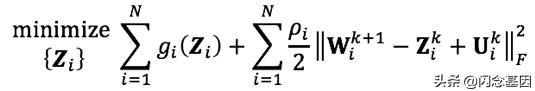 文章插图
文章插图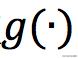 文章插图
文章插图的 指示函数 , 其解析解是:
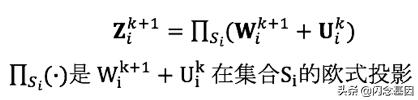 文章插图
文章插图
- 深度|iPhone12到底值得买吗 深度体验一周我发现了这些
- 采用|iPhone12mini和iPhone7深度对比:值得升级吗
- 设计|未来创意拒绝被垄断:欧拉共创成果深度解读!
- X50|vivo X50 Pro+深度测评:全能影像机皇登场
- 广度|华住创始人季琦:深度重要于广度
- NeurIPS 2020论文分享第一期|深度图高斯过程 | 深度图
- iPhone12 mini|从华为P30换成iPhone12mini,深度体验一周,优缺点很明显
- 建筑|国产第一台掘进机模型亮相“2020长江·三峡建筑产业博览会”
- 华为|华为Hicar一个月深度使用体验(途虎定制)
- 深度|专为年轻人打造的高端机 Redmi K30S至尊纪念版深度实测
