数据扩增技术如何实现正 margin 距离？( 二 ) 摘要数据扩增技术可以显著提

1.2 相关工作数据扩增技术旨在通过有限数量的输入数据扰动来提高模型的鲁棒性，鲁棒的优化方法还需要与经验风险最小化问题相联系。我们的工作与 Xu 的联系尤其紧密，这表明正则化 SVM 与线性分类的鲁棒性相关性较大。我们的工作也可以看作是在数据扩增技术里对于分类器的对抗扰动鲁棒性的量化研究。最近许多工作都从几何角度分析了各种分类器对于对抗性扰动的鲁棒性影响。Fawzi 引入了半随机噪声的概念，并根据决策边界的曲率研究了分类器对该噪点数据的鲁棒性。 Moosavi-Dezfooli 也将分类器的鲁棒性与其决策边界的局部曲率相关联，并提供了对神经网络决策边界曲率的经验性分析。 Fawzi 将分类器的鲁棒性与其经验风险相关联，并表明去保证最坏情况下的鲁棒性比对随机噪声的鲁棒性要困难得多。
我们的工作旨在量化数据扩增技术以保证经验风险最小化问题中的 margin 距离。我们首先分析线性可分离数据的线性分类问题，然后将结论扩展到非线性分类问题中。尽管我们可以通过二次编程的方法找到具有最大 margin 距离的线性分类器，但是将其推广到非线性分类器是非常困难的。如果这是神经网络的一项简单任务，那么对抗样本的问题将不复存在。因此，线性分类器是我们研究数据论证的有价值的切入点。
接下来，我们回顾线性分类的一些背景。我们假设可以设计算法 A ，该算法可以解决线性分类器集上的经验风险最小化问题。假设 S 是线性可分离的，线性分隔符 h∈H（S）的 margin 边距定义如下：
定义 1：线性分隔符 h（x）= sign（hw ， xi + b）与相关超平面 H 的边距为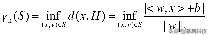
文章插图
如果 S 是线性可分离的，则存在一个线性分类器 h ? 对应于（w ? ， b ?），其最大 margin 边距为 γ? 。在本项工作中，我们将会分析未经正则化训练的 ERM 边距。 S 代表真实的数据集，为了达到一定的 margin 距离，我们创建了人工数据集 S0 。然后假设存在一种算法，该算法可以输出数据扩增后的数据集 S aug 。我们将分析相对于真实训练数据 S 的 margin 距离，如果 S 是线性可分离的，并且我们不添加任何人工噪点数据，则某些 h∈H(S)的 margin 距离为 0 。如果能够正确设计人工数据集 S0 ，那么我们希望 S aug 仍然是线性可分离的，并且任何 h∈H（S aug）相对于 S 都具有正 margin 距离。以下是这一想法的形式化表现：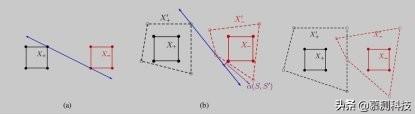
文章插图
实心点代表真实数据点，空心点代表人工数据点。真实数据和扩增数据的凸包分别由实线和虚线表示。分类器以蓝色显示。（a）如果没有进行数据扩增，我们可以获得零 margin 距离的分类器。（b）合理的数据扩增可以保证正 margin 距离。（c）大量数据点扩充可能会破坏线性可分离性。
定义 2：相对于原始数据 S ，扩增数据集 S aug 的线性分隔符的最坏情况下 margin 距离定义为：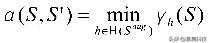
文章插图
我们着重探讨以下问题：我们如何设计 S’以使 α（S ， S’）尽可能大？我们分析起码 S’多大才能确保 α（S ， S’）为正。我们推导出| S’ | > d 是确保最坏情况下保证 margin 距离为正的必要条件。此外，如果 S’是通过 S 的有界扰动形成的，则需要| S’| ≥| S | 条件来保证正 margin 距离。之前我们分析了由半径为 r 的 S 的球面随机扰动形成 S’的设计思想，该设计反映了实际的随机噪声扰动。我们证明，如果 r 的校准不佳，则需要成倍的扰动来达到接近 γ? 的 margin 距离。但如果 r 设置正确，则具有| S’ |就足够了。
二线性分类器2.1 数据扩增规模度量假设 S 与最大余量 γ? 是可线性分离的。我们希望确定所需的 S’大小，以确保 α（S ， S’）> 0 。
定理 1. 如果| S’ |
因此，我们至少需要增加 d + 1 个点，才能确保正 margin 距离。目前我们希望了解使用数据扩增可能产生的 margin 距离大小，于是我们有以下引理。
引理 1.设 γ? 为 S 上的最大余量。对于所有 S’?Rd ， α（S ， S’）≤γ? 。
实际上，如果我们知道最大 margin 距离下的超平面，那么 d + 1 点就足以实现 α（S ， S’）=γ? 。
定理 2. 固定（n ， m）∈N2 并且 r>0 。然后| X + | = n 和| X- | = m ，因此，如果 S’?Sr ，并且| X’ + |
下图阐述了这个定理。给定 r ，我们选择 X +置于抛物线 P 上，以使这些点处的切线与其他点的距离至少为 r 。我们选择 X- ，使其在 x 轴下方足够远，对这些切线将 X +与 X aug 进行线性区分。假设我们不增加点 s∈X + ，该点的切线将 X +与 X aug 线性分开，而与 s 的距离为 0 。因此，我们需要在 X +的每个点上进行扩增，以保证正 margin 距离。