云台壹号简析机器学习中的分类回归树云台壹号认为

云台壹号认为，分类回归树（classification and regression tree ， CART）既可以用于预测离散变量（即分类问题），也可用于预测连续变量（即回归问题）。对于存在较强非线性关系的问题，通过分类回归树往往可以获得较好的结果。
文章插图
分类回归树的生成方法
分类回归树的生成方法是什么？某云台壹号相关人士表示，举个例子，假设我们得到了一个明星基金经理的持仓，希望了解该明星基金经理的持股偏好。我们选取了三个指标进行判断：净资产收益率（ROE）、净利润率和市盈率。
其中，解释变量X包含了所有股票以上三个指标的数值，目标变量Y表示基金经理是否持有该股票（1表示持有， 0表示不持有）。可以通过分类回归树（classification and regression tree）来解决这个问题。该云台壹号相关人士如是说。
一个分类回归树包含三类节点：根节点（root node）、决策树节点（decision node）和终节点（terminal node），见下图。根节点是位于树最顶端的节点，终节点是不包含分支的节点，其它节点均为决策节点。
云台壹号认为，构建分类回归树的关键步骤是分支（bifurcate）。分支是将一个节点拆分为两个子节点的过程。每一个分支包含两个要素：变量X ，和切分值C（cutoff value）。在给定X和C的情况下：将X≤C的样本，分到左边的子节点；将X＞C的样本，分到右边的子节点。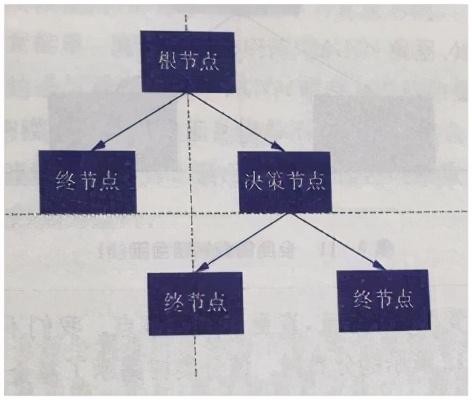
文章插图
确定分类回归树的分类误差
对于每一个节点，都可以计算一个分类误差（classification error）。分类回归树的构造方法要求子节点分类误差的和小于父节点。当子节点的误差与父节点的误差，小于预先设定的阈值时（即分支难以显著降低误差），则不再进行分支，该节点成为终节点。
回到之前的例子中，该云台壹号相关责任人表示，首先要确定的是根节点的分支，即选择是的分类误差最小的一个指标和该指标的切分值。假设经过计算，选择的指标为净资产收益，切分值为20% ，则相应的分支如图所示。
经过一次分支，所有的股票分为两类，一类是ROE小于或者等于20%的股票（左节点）；另一类是ROE大于20%的股票（右节点）。下一步，我们继续对左、右两个节点进行分支。
文章插图
【云台壹号简析机器学习中的分类回归树】云台壹号确切表示，假设在计算左节点的时候，无论哪个指标或切分值均无法显著降低分类误差。因此左节点就成为终节点。对于分类问题，终节点的值为样本中目标变量的众数。比如， ROE小于或等于20%的所有股票中，大部分没有被基金经理所持有，该终节点的值为0 。至此，分类回归树的结构如下图所示。
接下来，需要对右侧节点进行分支，直至达到终节点。我们不再赘述分支过程，假设最后我们得到了如下图所示的分类树。该分类树揭示了基金选择股票的倾向性：高ROE、高净利润率和低市盈率。如果未来有某个股票满足ROE高于20% ，净利润率高于15%和市盈率低于或等于30 ，则我们可以预期基金经理有较大概率会买入该股票。
“以上是一个利用分类回归树进行分类的例子。分类回归树的算法，经过一些调整，同样可以用于处理回归的问题。此时，分类回归树的终节点为其中样本的目标变量的均值。 ”该云台壹号相关人士总结到。