雷达图在数据可视化中的应用价值( 二 ) 编辑导语：雷达图

多维度往往意味着不同的度量单位，而雷达图从同一个中心点出发的轴又要求度量一致，不一致的度量会导致同一位置的点所表达的数据意义不一致。
现在有这么一个31岁的人，他的身高是160厘米体重是64公斤，我们想了解他在中青年（30-39岁）群体中的身高和体重水平，其中已知身高在150-200厘米内，体重在40-100公斤内。
从这边可以看到3个维度，分别是年龄、身高、体重，而这3者又带来3种不同的度量单位。如果不对度量进行统一处理，可视化成图如下所示，非常难以理解为什么160厘米和31岁处于同一梯度的点，而64公斤却比他们高，这样的雷达图不具备分析价值。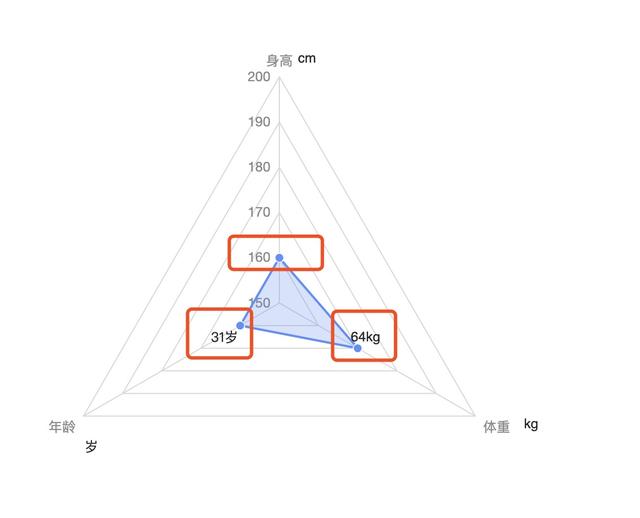
文章插图
那么我们怎么来完成这一度量统一的转化呢？
——这里就需要通过一定的公式进行转化。
什么样的公式才能适合这一转化过程呢？
雷达图有一个基础的认知，所表达的值是不同维度里的占比、或者处于该维度里哪一个范围。这就要求所提供的公式是一个可以划分范围或者确定排名的，通过这个公式，将不同的数据标准化定义下来。
下面通过对“年龄、身高、体重”的统一度量的公式来看下这个转化过程，统计学中有一个公式——平均值加减一组标准差，可以通过描述样本的离散程度来划分范围：

平均值为X ，标准差为S
平均值+一组标准差是该样本大部分值的上限，即X+S
平均值-一组标准差是该样本发部分值的下限，即X-S

通过“上限值”和“下限值”可以划分3个区间， “低于下限”、“上限和下限之间”、“高于上限”3个区间，样本中大部分的值处于区间“上限和下限之间” ，而“低于下限”和“高于上限”两个区间内的值就是异常值。
上述就是我们所要用到的理论公式，下面我们把具体的值代入其中：
已知中青年年龄段人身高的平均值是174 ，标准差是10 ，那么我们就可以得到3个区间“<164”、“164～174”、“>174” ， 3个区间对应的评分是1、2、3；而我们想要观察对象的身高是160 ，处于“<164”的区间，评分为1 。
同理，已知中青年年龄段人体重的平均值为73 ，标准差13 ， 3个区间为“<60”、“60-86”、“>86” ，已知中青年年龄段人年龄的平均值为34 ，标准差3 ， 3个区间“<31”、”31-37”、”>37” ，代入想要观察对象的体重和年龄数据得到评分为2 ， 2可得到年龄、身高、体重的三项评分为2、1、2 。
通过雷达图就可以大致对这个人的身高和体重水平有个简单的判断，这个人的年龄和体重处于中青年中的常见范围内，而身高则处于异常范围。
对比统一度量前后的雷达图，就可以明白统一度量后的雷达图才能更准确的体现这个人的年龄、身高和体重在中青年段人群中的所处范围。

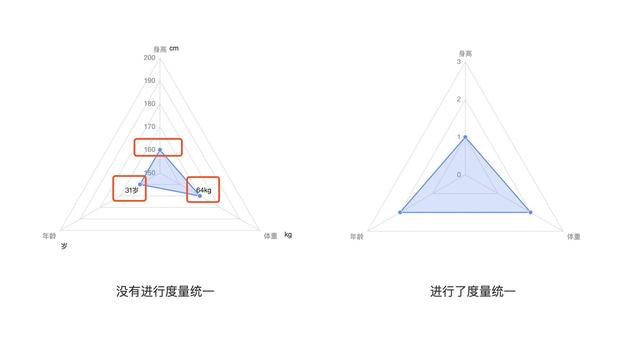文章插图
上面的公式只是一种非常简单的统一度量的公式，实际在工作中我们用到的公式会复杂的多，包括运用到加权、归一、收敛等数据统计方法。
通过对维度和度量的了解，可以认为雷达图的组成是一个递进过程的，首先需要有一组多维度的数据组，维度数需要是3个或3个以上；
其次需要通过选择一定的公式将不同维度的多个度量单位转换成“统一度量” ，在这个过程中，需要有一个可衡量的规则将不同维度的数据标准化；
【雷达图在数据可视化中的应用价值】最后将统一度量后的数据转化成图，就得到了可以被应用的雷达图，表达了对象的综合能力在对应维度里的一个占比情况或者排名。
二、雷达图具体的运用价值了解完什么是雷达图以后，我们就可以来讨论雷达图实际的运用价值，具体可以分两部分，一是在描述单一对象上的运用，二是在对比多个对象上的运用。
1. 雷达图在单一对象上的运用文章开头场景中用雷达图描述某个客服的综合能力就是一次典型的运用了“雷达图”来描述单个对象属性，为什么雷达图可以用来描述某个对象的属性呢？
从雷达图的定义可以看出，雷达图是一组多维度数据组的图形化表达，而一个对象的属性往往是多维度的。
另外，人对于描述性文字是没有一个明确的感知力的，比如这句对下图客服表现的描述，销售额1w ，响应时间3秒，询单转化率95% 。
单独从文字描述来看，是非常空洞的，我们无法准确判断这个客服的能力，销售额1w是多还是少，响应时间3秒是响应快还是慢，询转95%又是否足够高？